Lezione 8: Equazioni differenziali

Leonardo CarminatiMaurizio Tomasi

[La pagina con la spiegazione originale degli esercizi si trova qui: https://labtnds.docs.cern.ch/Lezione8/Lezione8/.]

In questa lezione introdurremo alcuni metodi per la risoluzione di equazioni differenziali ordinarie. Implementeremo la risoluzione numerica di queste equazioni con i metodi di Eulero e di Runge-Kutta.

Per risolvere l’esercizio vedremo come è possibile definire le principali operazioni algebriche per classi della STL come std::vector o il nuovo std::array. Questo ci permetterà di realizzare i metodi di integrazione di equazioni differenziali usando una notazione vettoriale, molto simile al formalismo matematico.

Introduzione a std::array

La STL fornisce varie implementazioni del concetto di “array”. Finora abbiamo sempre usato il tipo std::vector, che è una versione più potente degli array del C. Le due variabili array e vec nell’esempio contengono gli stessi elementi:

double array[] = {1.0, 2.0, 3.0};
std::vector<double> stl_vec{1.0, 2.0, 3.0};

ma la variabile stl_vec ha più funzionalità:

Oltre a std::vector, la STL offre la possibilità di usare std::array, che si comporta esattamente come std::vector a parte queste differenze:

Il testo originale degli esercizi di Carminati assume che negli esercizi di oggi si usi std::vector, ma il testo qui sotto vi mostrerà invece come usare std::array, perché rende impossibile alcuni errori che gli studenti tendono a fare.

Questo è il modo in cui si usa:

// Notare che bisogna indicare il numero di elementi
// *dentro* le parentesi angolari <> del template!
std::array<double, 3> stl_arr{1.0, 2.0, 3.0};

La scrittura array<double, 3> può sembrare strana: finora abbiamo sempre visto nelle parentesi angolari <> dei template tipi come double oppure int, ma il C++ permette anche di specificare valori come parametri dei template.

È poi possibile implementare codice come se si stesse usando un oggetto di tipo std::vector:

for(int i{}; i < ssize(stl_arr); ++i) {
  // Ok anche `stl_arr[i]`, ma non controlla la
  // correttezza di `i`
  fmt::println("Valore #{}: {}", i, stl_arr.at(i));
}

ma è vietato chiamare metodi come stl_arr.push_back(5.0), perché la dimensione dell’array non cambia mai!

Se si vogliono definire funzioni che operano su un array, nel template bisogna non solo indicare <typename T> come nel caso di std::vector, perché qui anche la dimensione dell’array è un parametro (che purtroppo va indicata come size_t anziché int 🙁):

// Using `int` instead of `size_t` doesn’t work…
template <typename T, size_t n>
void print(const std::array<T, n> & arr) {
  // …
}

Notate che T è dichiarata come typename, perché questo parametro rappresenta un tipo come double oppure int, mentre n è un numero (size_t è un intero senza segno), perché questo non deve essere un tipo bensì un valore come 2, 5, 14…

Esercizio 8.0 - Algebra vettoriale

Come prima cosa, proviamo a dotare il tipo std::array della STL di tutte le funzionalità algebriche che ci possono essere utili, definendo opportunamente gli operatori +, *, /, +=. Dal momento che non possiamo modificare gli header files e i files di implementazione della classe std::array, implementiamo questi operatori come funzioni libere in un header file apposito da includere quando necessario. Potete trovarne un esempio qui.

Notate la presenza della funzione test_array_operations(), che verifica la correttezza delle operazioni su std::array. Usando solo numeri interi per le componenti dei vettori, non c’è bisogno di invocare la nostra solita funzione are_close() perché in questo caso la variabile double opera senza arrotondamenti.

Ovviamente, per eseguire i test basta invocarli all’inizio di main(), come al solito:

#include "array_operations.h"
#include <array>

int main() {
  test_array_operations();
}

Verificate che venga stampato il messaggio che certifica il successo dei test!

Esercizio 8.1 - Risoluzione tramite metodo di Eulero

Nel primo esercizio implementeremo un codice per la risoluzione numerica dell’equazione differenziale che descrive il moto di un oscillatore armonico tramite il metodo di Eulero. Gli obiettivi principali di questo esercizio sono due:

  1. Studiare l’andamento della posizione in funzione del tempo t (per t che va da 0 a 70 secondi) per un fissato passo di integrazione h (si potrebbe costruire un grafico, per esempio) e confrontare l’errore commesso con la soluzione esatta.

  2. Studiare l’andamento dell’errore che si commette utilizzando il metodo di Eulero quando confrontiamo la soluzione approssimata con la soluzione esatta nell’istante t = 70 s in funzione del passo di integrazione h in un intervallo compreso tra 0.1 e 0.001.

Per testare il metodo, risolviamo l’equazione differenziale:

\frac{\mathrm{d}}{\mathrm{d}t} \begin{pmatrix}x\\v\end{pmatrix} = \begin{pmatrix}v\\-\omega_0^2 x\end{pmatrix},\quad x(0) = 0, \quad v(0) = 1\,\text{m/s}, \quad \omega_0 = 1\,\text{s}^{-1},

mettendo in grafico il valore della x in funzione del tempo t ed eventualmente anche il suo errore rispetto alla soluzione esatta del problema, che è x(t) = \sin (t). Si consiglia di svolgere l’integrazione per un certo numero di periodi, in modo da vedere se l’ampiezza di oscillazione rimane costante. Integrare fino a t = 70\,\text{s} permette di vedere circa 10 periodi.

Il metodo di Eulero

Consideriamo la seconda legge della dinamica di Newton:

a = \frac{\mathrm{d}^2 x}{\mathrm{d}t^2} = \frac{F}m.

Essa è un’equazione differenziale del secondo ordine che può essere ridotta ad un’equazione differenziale del prim’ordine introducendo la variabile velocità:

\begin{aligned} \frac{\mathrm{d} x}{\mathrm{d}t} &= v,\\ \frac{\mathrm{d} v}{\mathrm{d}t} &= \frac{F}m. \end{aligned}

Il metodo di Eulero consiste nel calcolare lo stato della soluzione al tempo t + h dato quello ad un tempo t tramite le espressioni:

\begin{aligned} x(t + h) &\approx x(t) + h \cdot \dot{x}(t) = x(t) + h \cdot v,\\ v(t + h) &\approx v(t) + h \cdot \dot{v}(t) = x(t) + h \cdot \frac{F}m. \end{aligned}

Struttura del programma

Struttureremo la soluzione del problema in modo simile a quanto fatto nelle precedenti lezioni su ricerca degli zeri e integrazione numerica:

Per comodità possiamo mettere tutte queste classi nello stesso header file che potrebbe avere l’aspetto seguente:

#pragma once

#include "array_operations.h"
#include <cmath>

// classe astratta, restituisce la derivata valutata nel punto x
// di una funzione a `n` dimensioni, dove `n` è un parametro del
// template
template <size_t n> class FunzioneVettorialeBase {

public:
  virtual std::array<double, n> Eval(double t,
                                     const std::array<double, n> &x) const = 0;
};

// caso fisico concreto, oscillatore armonico a 1 dimensione,
// che corrisponde ad una dimensione 2 nello spazio delle fasi
// (notare `<2>` alla fine di `FunzioneVettorialeBase`: questa
// classe *non* è template, perché sia il tipo T che il numero n
// sono definiti ed univoci: `double` e `2`).
class OscillatoreArmonico : public FunzioneVettorialeBase<2> {
public:
  OscillatoreArmonico(double omega0) : m_omega0{omega0} {}

  std::array<double, 2>
  Eval(double t,
       const std::array<double, 2> &x) const override {
    // Implementare il metodo
  }

private:
  double m_omega0;
};

// classe astratta per un integratore di equazioni differenziali
// (Eulero, Runge Kutta, etc.) a N dimensioni
template <size_t n> class EquazioneDifferenzialeBase {
public:
  virtual std::array<double, n>
  Passo(double t, const std::array<double, n> &x, double h,
        const FunzioneVettorialeBase<n> &f) const = 0;
};

// integratore concreto, metodo di Eulero a N dimensioni
template <size_t n> class Eulero : public EquazioneDifferenzialeBase<n> {
public:
  std::array<double, n>
  Passo(double t, const std::array<double, n> &x, double h,
        const FunzioneVettorialeBase<n> &f) const override {
    // Implementare il metodo: basta una riga di codice per Eulero!
  }
};

// Test del metodo di Eulero

inline double are_close(double a, double b, double eps = 1e-7) {
  return abs(a - b) < eps;
}

inline void test_euler() {
  // Verifica la correttezza del metodo di Eulero integrando
  // l'oscillatore armonico con ω₀=1 rad/s e verificando che
  // al tempo t=0.9 s posizione e velocità coincidano con
  // la soluzione del codice Julia all'indirizzo
  // https://ziotom78.github.io/tnds-notebooks/lezione08/#esercizio_81_metodo_di_eulero
  Eulero<2> my_euler{};

  OscillatoreArmonico osc{1.};

  const double tmax{0.91}; // È più sicuro usare qualcosa di più di 0.9
  const double h{0.1};
  array<double, 2> x{0., 1.};
  double t{};

  // `lround` è come `round`, ma arrotonda sempre verso il basso
  const int num_of_steps{(int) lround(tmax / h)};

  // evoluzione del sistema fino a 0.9 s
  for (int step{}; step < num_of_steps; step++) {
    x = my_euler.Passo(t, x, h, osc);
    t = t + h;
  }

  // Questi sono i numeri prodotti dal codice Julia. Verifichiamo fino
  // alla sesta cifra, perché i numeri stampati dal programma Julia
  // usavano questa convenzione
  assert(are_close(x[0], 0.817256, 1e-6));
  assert(are_close(x[1], 0.652516, 1e-6));
}

Una volta implementate le classi (l’implementazione di Eulero è semplicissima se si usano le operazioni di algebra vettoriale), un possibile programma per risolvere l’esercizio è il seguente:

#include "array_operations.h"
#include "equazioni_differenziali.h"

#include "fmtlib.h"
#include "gplot++.h"
#include <string>

int main(int argc, char *argv[]) {
  test_array_operations();
  test_euler();

  if (argc != 2) {
    fmt::println(stderr, "Uso: {} PASSO", argv[0]);
    return 1;
  }

  Eulero<2> my_euler{};

  OscillatoreArmonico osc{1.};

  const double tmax{70.};
  const double h{stof(argv[1])};
  double t{};
  array<double, 2> x{0., 1.};

  const int num_of_steps{(int)lround(tmax / h)};

  // evoluzione del sistema fino a 70 s

  Gnuplot plt{};

  // Ho bisogno di costruire due vettori per poter poi
  // fare il plot. Qui uso "vector" anziché "array",
  // perché le due liste potrebbero essere molto grandi
  // e si rischierebbe quindi di riempire lo stack.
  //
  // Notare che uso `()` anziché `{}` per passare i
  // parametri del costruttore, perché voglio
  // specificare il *numero di elementi* del vettore!
  std::vector<double> list_of_t(num_of_steps);
  std::vector<double> list_of_x(num_of_steps);

  for (int step = 0; step < num_of_steps; step++) {
    // Salva le coordinate del punto (t, x) per
    // fare poi il grafico
    list_of_t.at(step) = t;
    list_of_x.at(step) = x[0];

    // Stampa i risultati in forma di tabella
    // (da fare sempre! aiuta nel trovare errori)
    fmt::println("{:.1f} {:.6f} {:.6f}", t, x[0], x[1]);

    // “Avanza” di un passo `h` la soluzione in `x`
    x = my_euler.Passo(t, x, h, osc);
    t = t + h;
  }

  // Ora si può produrre il grafico

  std::string filename{"euler.png"};
  plt.redirect_to_png(filename);
  plt.plot(list_of_t, list_of_x);
  plt.set_xlabel("Tempo [s]");
  plt.set_ylabel("Oscillazione [m]");
  plt.show();

  // È sempre bene dare all'utente un feedback di ciò che
  // si è fatto: in questo modo l'utente saprà quale file aprire!
  fmt::println("Finito, il risultato è nel grafico '{}'", filename);

  return 0;
}

Come al solito, potete installare la libreria fmtlib usando lo script install_fmt_library: scaricatelo nella directory dell’esercizio ed eseguitelo con sh install_fmt_library, oppure eseguite direttamente questo comando:

In alternativa, scaricate questo file zip nella directory dell’esercizio e decomprimetelo. Le istruzioni dettagliate sono in questa pagina.

Il codice sopra usa la libreria gplot++ per salvare il grafico della soluzione in un file PNG. Se invece volete usare ROOT, queste sono le righe da aggiungere alla seconda parte del main:

TApplication myApp{"myApp", 0, 0};
TGraph *myGraph{new TGraph()};

for (int step{}; step < num_of_steps; step++) {
    myGraph->SetPoint(step, t, x[0]);
    x = myEuler.Passo(t, x, h, osc);
    t += h;
}
print(t, x);

TCanvas *c{new TCanvas()};
c->cd();
string title{fmt::format("Oscillatore armonico (Eulero, h = {})", h)};

myGraph->SetTitle(title.c_str());
myGraph->GetXaxis()->SetTitle("Tempo [s]1");
myGraph->GetYaxis()->SetTitle("Posizione x [m]");
myGraph->Draw("AL");

myApp.Run();

Si riveda il solito esempio (qui) per l’uso dei TGraph di ROOT.

Risultati attesi

Il metodo di Eulero non è molto accurato; in effetti, con un passo di integrazione modesto si vede come esso possa risultare instabile, mostrando oscillazioni la cui ampiezza varia con il tempo. La figura sotto mostra l’andamento di x(t) con un passo di integrazione di 0.1 s:

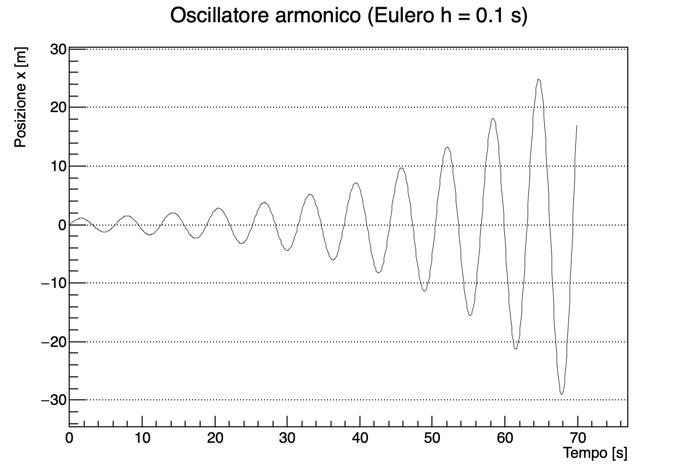
Per avere qualcosa di anche solo visivamente accettabile, bisogna andare a passi di almeno 0.0002 s:

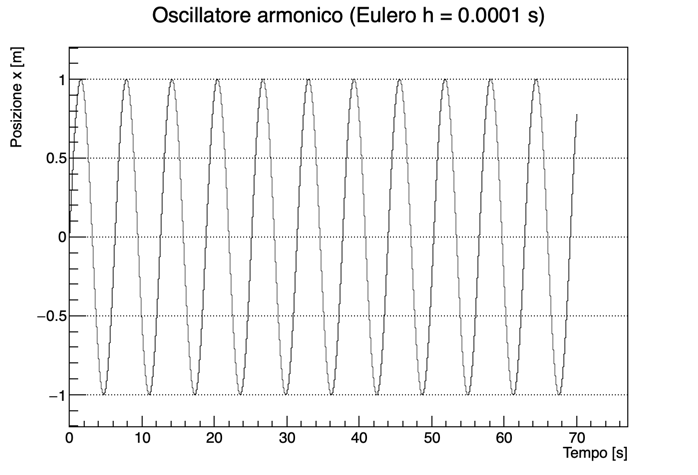
La figura seguente riporta l’errore accumulato dopo 70 s di integrazione per diversi valori del passo:

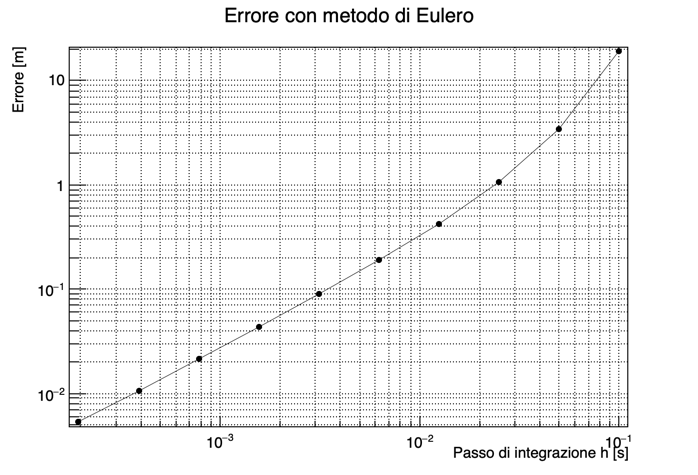
Si noti come la pendenza della curva sia 1 in una scala log-log, mostrando come l’errore ottenuto sia proporzionale al passo h.

Esercizio 8.2 - Risoluzione tramite Runge-Kutta (da consegnare)

Ripetere l’esercizio 8.1 con il metodo di risoluzione di equazioni differenziali di Runge-Kutta (del quarto ordine) e confrontare quindi in condizioni analoghe (t massimo e h) la stabilità dei due metodi.

Per svolgere l’esercizio, basterà realizzare una nuova classe concreta a partire da EquazioneDifferenzialeBase. Implementate anche un metodo test_runge_kutta() sulla falsariga di test_euler() per l’esercizio 8.1.

Il metodo di Runge-Kutta

Il noto metodo di Runge-Kutta è un metodo del quarto ordine ed utilizza la seguente determinazione dell’incremento:

\begin{aligned} k_1 &= \dot{x}(t, x),\\ k_2 &= \dot{x}\left(t + h / 2, x + k_1 \cdot \frac{h}2\right),\\ k_3 &= \dot{x}\left(t + h / 2, x + k_2 \cdot \frac{h}2\right),\\ k_4 &= \dot{x}\left(t + h, x + k_3 \cdot h\right),\\ x(t+h) &= x(t) + (k_1 + 2k_2 + 2k_3 + k_4)\frac{h}6. \end{aligned}

Cosa ci aspettiamo?

Il metodo di Runge-Kutta del quarto ordine è molto più preciso del metodo di Eulero: infatti produce oscillazioni molto stabili anche con un passo di integrazione di 0.1 s:

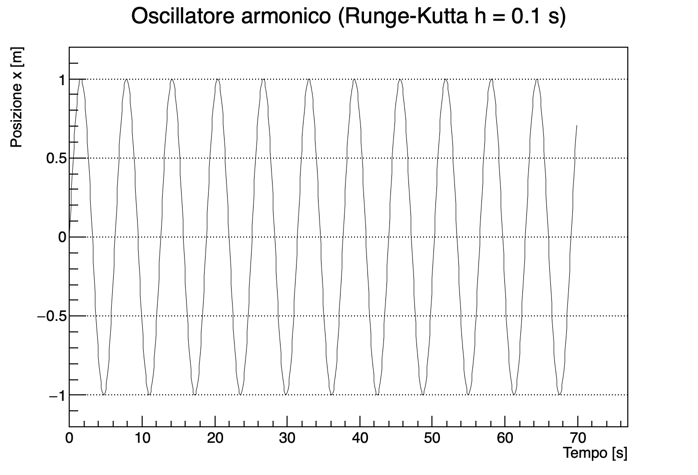
La figura seguente riporta l’errore accumulato dopo 70 s di integrazione per diversi valori del passo:

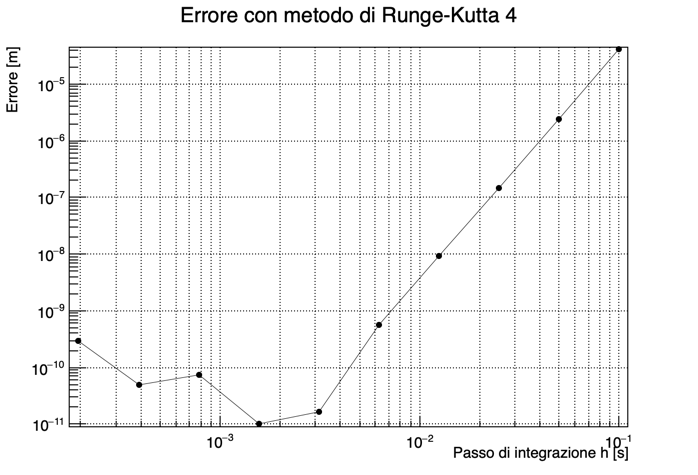
Si noti come la pendenza della curva nella sua parte iniziale sia 4 in una scala log-log, mostrando come l’errore ottenuto sia proporzionale a h^4. Quando l’errore di troncamento del metodo diventa minore degli errori di arrotondamento della macchina si vede che non c’è più alcun miglioramento nel ridurre il passo, anzi, il maggior numero di calcoli richiesto risulta in un peggioramento globale dell’errore.

Esercizio 8.3 - Moto del pendolo (da consegnare)

Incominciamo ora con una carrellata di interessanti applicazioni dei metodi che abbiamo appena studiato. In questo esercizio proveremo ad implementare la risoluzione dell’equazione del moto del pendolo: per prima cosa possiamo provare a fare un grafico dell’andamento dell’ampiezza dell’oscillazione in funzione del tempo. La cosa più interessante che possiamo studiare con questo codice è l’andamento del periodo di oscillazione in funzione dell’ampiezza di oscillazione: in questo modo possiamo verificare che per angoli grandi le oscillazioni non sono più isocrone. La struttura logica dell’esercizio dovrebbe essere la seguente:

  1. Portare il sistema in una condizione iniziale (θ₀, 0);

  2. Far evolvere il sistema usando il metodo di Eulero o di Runge-Kutta con passo di integrazione h opportuno;

  3. Calcolare il periodo di oscillazione del pendolo;

  4. Riportare il sistema ad una condizione iniziale con ampiezza θ₀ variata e ripetere la sequenza di operazioni

Si suggerisce di far variare θ₀ tra 0.1 e 3 radianti, in passi di 0.1 radianti.

Il moto del pendolo

L’equazione del pendolo è data dalla relazione

\frac{\mathrm{d}^2\theta}{\mathrm{d}t^2} = -\frac{g}{l}\sin\theta,

dove g = 9.8\,\text{m/s}^2 è l’accellerazione di gravità sulla superficie terreste, mentre l è la lunghezza del pendolo.

L’equazione differenziale si può approssimare con quella di un oscillatore armonico per piccole oscillazioni, \sin\theta\sim\theta. In tal caso, le oscillazioni risultano isocrone, cioè con periodo indipendente dall’ampiezza delle oscillazioni. Questa però è solo un’approssimazione, e per grandi oscillazioni bisogna usare l’equazione esatta.

Calcolo del periodo

In questo caso l’integrazione numerica dell’equazione differenziale non si può effettuare per un tempo predefinito, ma deve essere portata avanti fino a quando non si raggiunge una condizione compatibile con l’aver terminato l’oscillazione.

Un frammento di codice che implementa questo algoritmo è il seguente:

double A{0.1 * (i + 1)};
double v{};
double t{};
std::array<double, 2> x{-A , v} ;
while (x[1] >= 0) {
    v = x[1];
    x = myRK4.Passo(t, x, h, osc);
    t = t + h;
    fmt::println("{} {} {}", A, x[0], t);
}
t = t - v * h / (x[1] - v);

// Il periodo è il *doppio* del tempo che abbiamo trovato!
double period{2 * t};

Controllate la formula di interpolazione!

Risultati attesi

La figura illustra il periodo al variare dell’ampiezza per un pendolo con l = 1\,\text{m}:

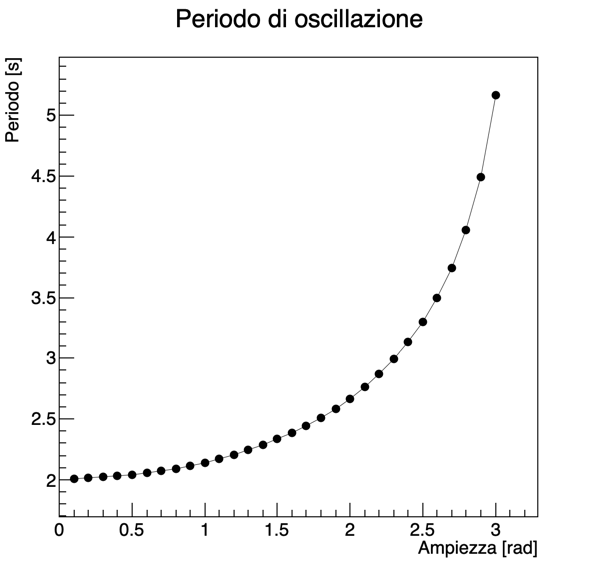
Si noti come per piccole oscillazioni il periodo sia effettivamente quello atteso dall’approssimazione dell’oscillatore armonico:

T = \frac{2\pi}{\sqrt{\frac{g}l}} \approx 2.007\,\text{s},

ma aumenti significativamente per grandi ampiezze.

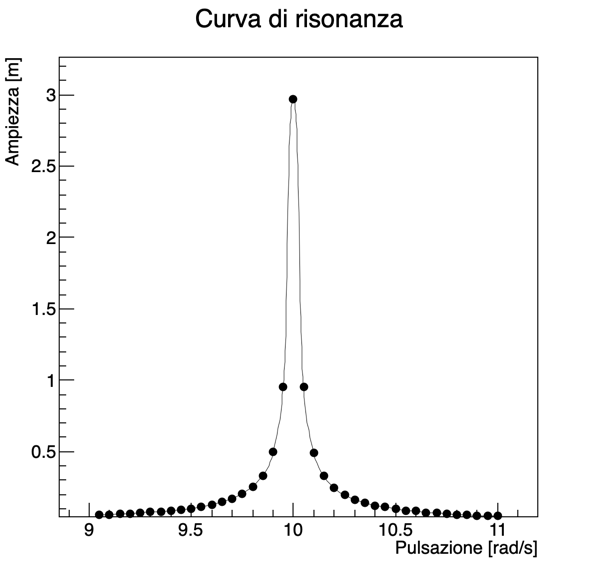
Esercizio 8.4 - Oscillazione forzate e risonanza (da consegnare)

Implementare la risoluzione dell’equazione di un oscillatore armonico smorzato con forzante. Fare quindi un grafico della soluzione stazionaria in funzione della frequenza dell’oscillatore, ricostruendo la curva di risonanza. La struttura logica dell’esercizio dovrebbe essere la seguente:

Oscillatore armonico con forzante

L’equazione dell’oscillatore armonico smorzato con forzante è data dalla relazione

\frac{\mathrm{d}^2x}{\mathrm{d}t^2} = -\omega_0^2 x - \alpha \dot{x}(t) + a_0 \sin(\omega t).

Nell’esercizio proposto, utilizzare i seguenti valori iniziali: \omega_0 = 10\,\text{rad/s}, \quad \alpha = \frac1{30\,\text{s}}, \quad a_0 = 1\,\text{m/s}^2.

Risultati attesi

La figura seguente riporta l’andamento dell’ampiezza in funzione del tempo nel caso in cui la frequenza propria del sistema (ω₀) e quella della forzante (ω) coincidano: ω₀ = ω = 10 rad/s.

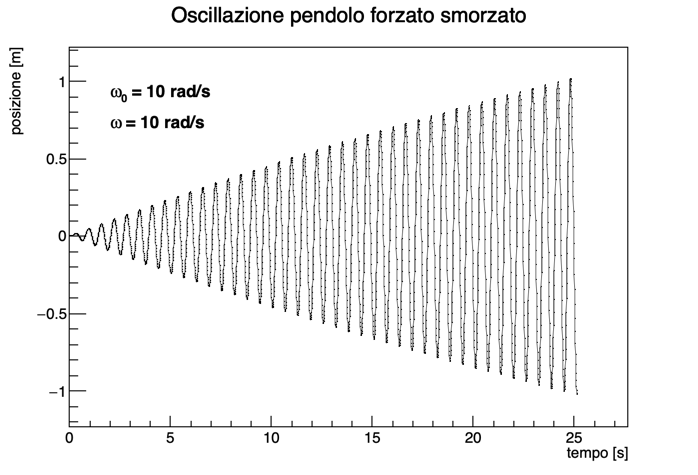
È bene ricordare che per determinare l’ampiezza bisogna aspettare che il transiente delle oscillazioni si esaurisca. Questo avviene con una costante di tempo pari a 1/α (ovvero, dopo un tempo 1/α l’ampiezza di oscillazione si riduce di un fattore 1/e).

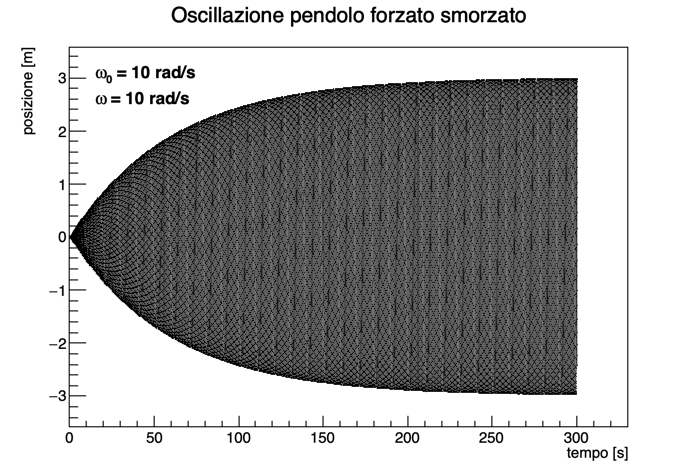
Si consiglia quindi di integrare l’equazione differenziale per un tempo pari ad almeno dieci volte 1/α, in modo da raggiungere una situazione in cui l’oscillazione è stabile, e poi valutare l’ampiezza. Anche in questo caso si può assumere di aver raggiunto il massimo dell’oscillazione nel momento in cui si trova un punto in cui la velocità cambia di segno.

Una curva di risonanza è illustrata in figura:

Esercizio 8.5 - Moto in campo gravitazionale

Implementare la risoluzione dell’equazione del moto di un corpo in un campo gravitazionale.

Moto in campo gravitazionale

Nell’implementare il moto di un corpo in un campo gravitazionale utilizzare le seguenti condizioni:

Ovviamente, essendo tutti voi studenti di fisica, non c’è alcun bisogno di ricordarvi che nel vostro codice le unità di misura devono essere consistenti… quindi non ve lo ricorderò! 😉

Risultati attesi

Nel caso di potenziale gravitazionale standard dovremmo ottenere una traiettoria di questo tipo:

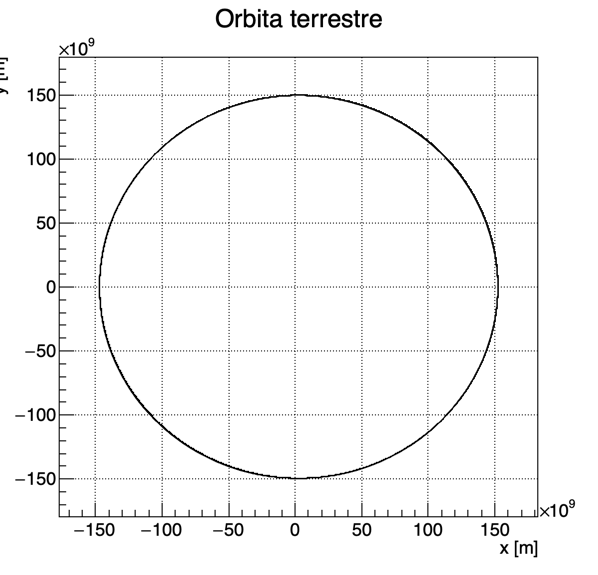
Aggiungendo un termine di perturbazione α/r³ al potenziale gravitazionale, la traiettoria diventa la seguente:

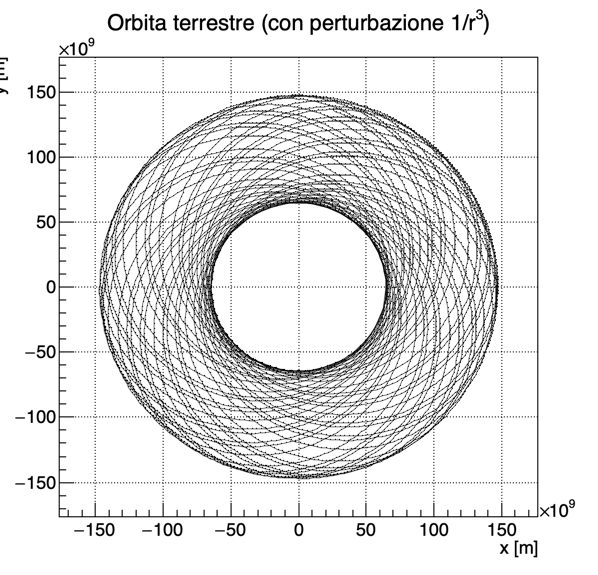
Visualizzare l’evoluzione temporale

In questo caso potrebbe essere interessante visualizzare l’evoluzione temporale della traiettoria della terra in modo dinamico. Per fare questo possiamo semplicemente visualizzare il grafico della traiettoria ogni volta che viene aggiunto un nuovo punto, introducendo un’attesa nel ciclo for per regolare la velocità dell’animazione: il C++ fornisce la funzione std::this_thread::sleep_for(), che richiede un tempo definito tramite le funzioni in <chrono>, quindi occorrono queste librerie:

#include <chrono>
#include <thread>

Per introdurre un ritardo prima di eseguire il ciclo seguente, bisogna quindi invocare sleep_for nel modo seguente:

Gnuplot gpl{};

// ...

const double plot_range{160e9}; // Maximum distance from the Sun

for (int npoint{}; npoint < nstep ; npoint++) {
  // Add the point, plot the graph and show the new frame
  gpl.add_point(x[0], x[1]);
  gpl.plot();  // Make the plot in memory (hidden from the user)
  // Be sure that the axes don't change during the animation
  gpl.set_xrange(-plot_range, plot_range);
  gpl.set_yrange(-plot_range, plot_range);
  gpl.show();  // Show the plot in the Gnuplot window

  // Wait for 1 ms
  std::this_thread::sleep_for(std::chrono::milliseconds(1));

  // Step to the next point
  x = integratore->Passo(t, x, h, f);
  t += h;
}

A partire dalla versione 0.9.0, gplot++ fornisce però il metodo redirect_to_animated_gif, che crea un file GIF animato contenente l’animazione; in questo caso non serve includere <chrono> o <thread>. Il metodo richiede questi parametri:

Con gplot++, il codice diventerebbe questo:

Gnuplot gpl{};

// ...
gpl.redirect_to_animated_gif("es8.4.gif", "800,600", 1);

const double plot_range{160e9}; // Maximum distance from the Sun

for (int npoint{}; npoint < nstep ; npoint++) {
  // Add the point, plot the graph and show the new frame
  gpl.add_point(x[0], x[1]);
  gpl.plot();  // Make the plot in memory (hidden from the user)
  // Be sure that the axes don't change during the animation
  gpl.set_xrange(-plot_range, plot_range);
  gpl.set_yrange(-plot_range, plot_range);
  gpl.show();  // Show the plot in the Gnuplot window

  // Step to the next point
  x = integratore->Passo(t, x, h, f);
  t += h;
}

Di seguito un esempio di file GIF creato con un termine aggiuntivo di forza espresso come F'(\vec r) = -\alpha G \frac{M_\odot\,M_t\,D_p}{r^4} \vec r, dove \alpha = 0.3 è un numero puro e D_p è la distanza Terra-Sole al perielio. Lo step usato per l’animazione è cinque giorni (ossia, h = 86\,400\,\text{s/day} \times 5\,\text{day}):

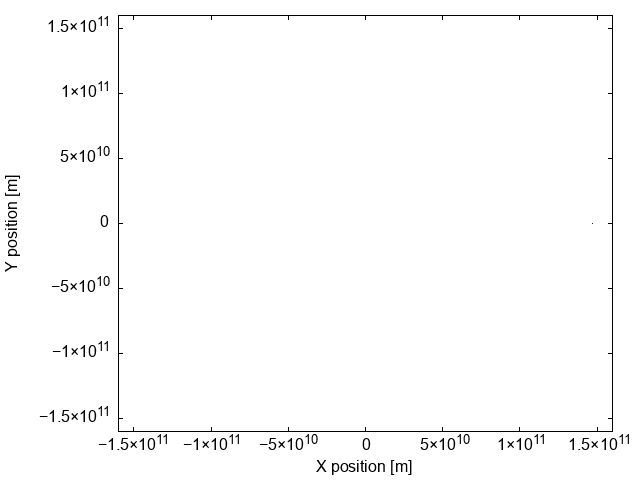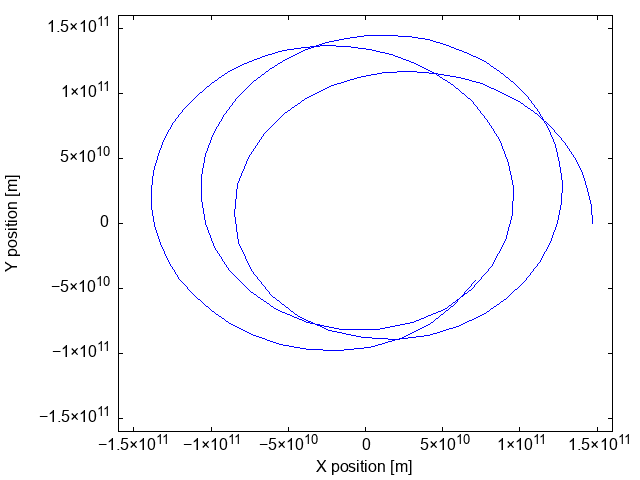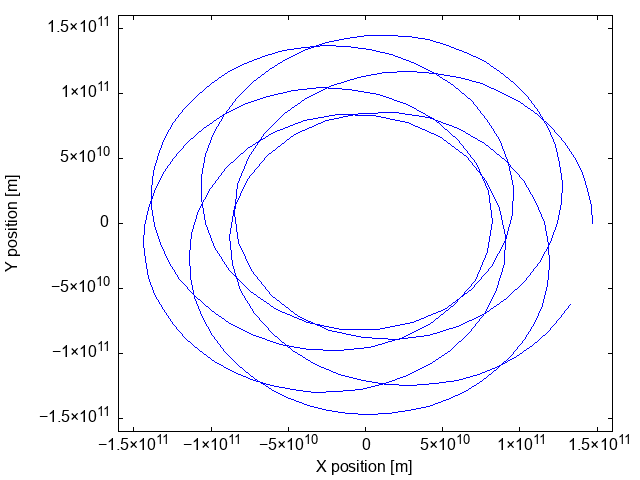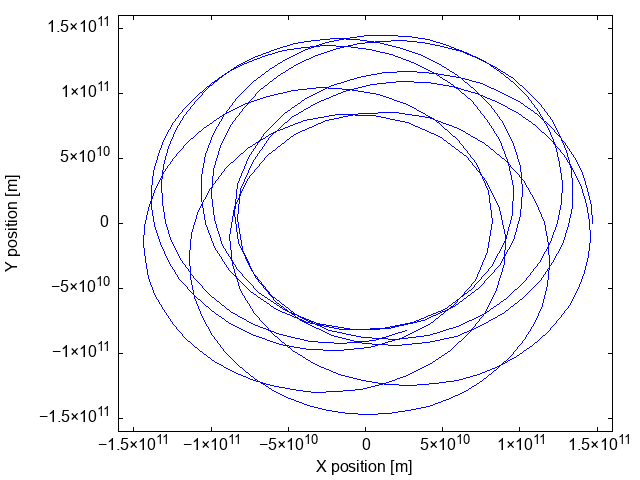
Se usate ROOT anziché gplot++, dovete includere anche TSystem.h perché ROOT deve sincronizzare le operazioni di disegno tramite gSystem->ProcessEvents():

#include "TSystem.h"

e il codice diventerebbe il seguente:

// creazione TGraph e TCanvas

TGraph tRosetta;
TCanvas CRosetta{"CRosetta", "CRosetta", 600, 600};
tRosetta.GetXaxis()->SetTitle("x (m)");
tRosetta.GetYaxis()->SetTitle("y (m)");

for (int npoint{}; npoint < nstep ; npoint++) {
  // add the point, plot the graph and update the view
  tRosetta.SetPoint(npoint, x[0], x[1]);
  tRosetta.Draw("ALP");
  CRosetta.Update();
  gSystem->ProcessEvents();

  // Wait for 1 ms
  std::this_thread::sleep_for(std::chrono::milliseconds(1));

  // Step to the next point
  x = integratore->Passo(t, x, h, f);
  t += h;
}

Potete ovviamente usare queste tecniche anche per gli esercizi precedenti.

Esercizio 8.6 - Moto di una particella carica in un campo elettrico e magnetico uniforme

Implementare la risoluzione dell’equazione del moto di una particella carica in un magnetico uniforme. Disegnare la traiettoria della particella e determinarne il diametro dell’orbita. Cosa succede se si aggiunge un campo elettrico con componente lungo l’asse z pari a E_z = -1000\,\text{V/m}?

Moto in campo elettrico e magnetico uniformi

Il moto di una particella carica in un campo elettrico e magnetico uniformi risente della forza di Lorentz e pertanto è descritto dall’equazione m\ddot{x}(t) = q E + q v\times B, che si può riscrivere in forma matriciale come \frac{\mathrm{d}}{\mathrm{d}t} \begin{pmatrix} x\\ y\\ z\\ v_x\\ v_y\\ v_z \end{pmatrix} = \begin{pmatrix} 0& 0& 0& 1& 0& 0\\ 0& 0& 0& 0& 1& 0\\ 0& 0& 0& 0& 0& 1\\ 0& 0& 0& 0& \frac{q}m B_z& -\frac{q}m B_y\\ 0& 0& 0& -\frac{q}m B_z& 0& \frac{q}m B_x\\ 0& 0& 0& \frac{q}m B_y& -\frac{q}m B_x& 0 \end{pmatrix} \begin{pmatrix} x\\ y\\ z\\ v_x\\ v_y\\ v_z \end{pmatrix} + \begin{pmatrix} 0\\ 0\\ 0\\ \frac{q}m E_x\\ \frac{q}m E_y\\ \frac{q}m E_z \end{pmatrix}. È un problema tridimensionale, e richiede quindi uno spazio delle fasi a sei dimensioni. Bisognerà quindi usare tipi std::array<double, 6>.

Consideriamo il moto nel piano (x, y) di un elettrone in un campo magnetico costante con i seguenti valori:

Questi parametri corrispondono grosso modo all’apparato sperimentale per la misura di e/m del laboratorio del II anno.

Risultati attesi

Per prima cosa potremmo cercare di disegnare la traiettoria nel piano (x, y):

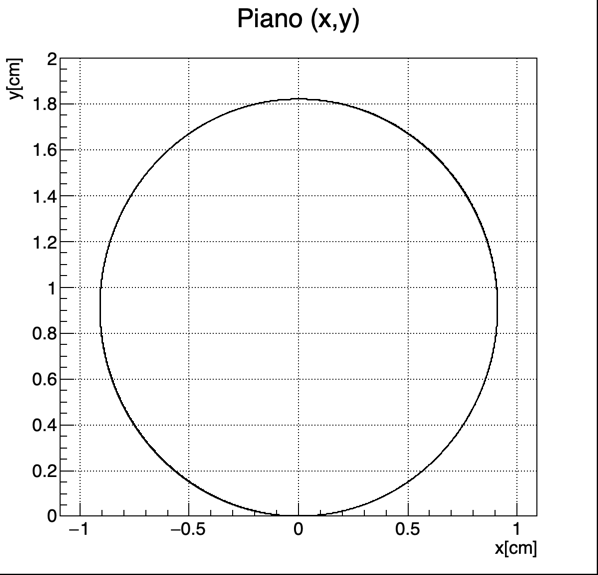
e poi (a titolo di esempio) l’andamento della coordinata z in funzione del tempo:

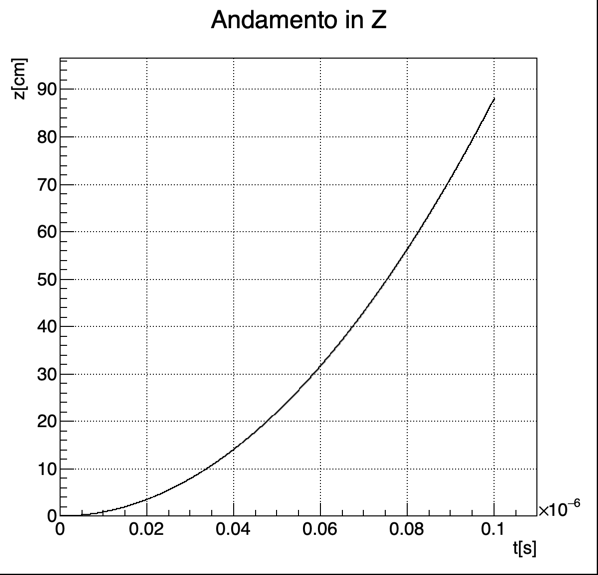
È infine possibile visualizzare la traiettoria della particella in tre dimensioni:

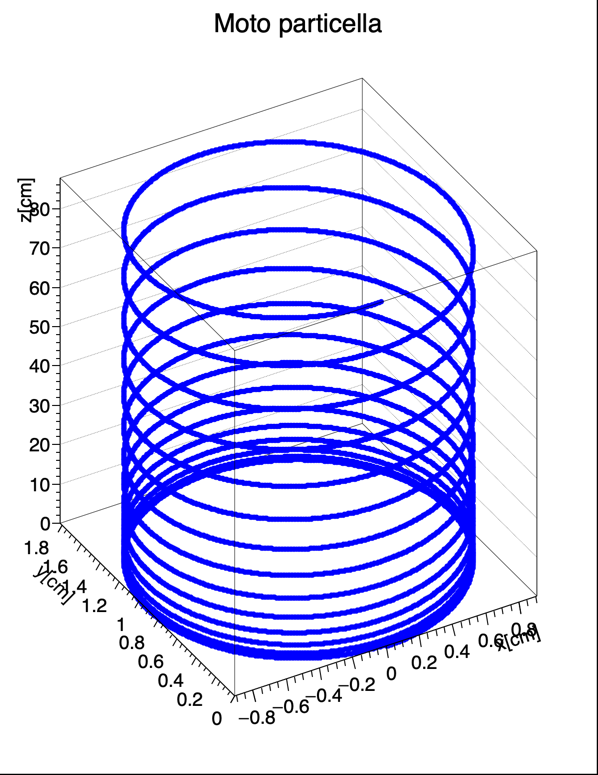
Per rappresentare la traiettoria dell’elettrone con gplot++ si può usare la funzione plot3d, salvando i punti della traiettoria in tre vettori di double. Con ROOT si può invece utilizzare la classe TGraph2D.

Errori comuni

Come di consueto, elenco alcuni errori molto comuni che ho trovato negli anni passati correggendo gli esercizi che gli studenti hanno consegnato all’esame: