TNDS

In questa lezione implementeremo dei programmi per risolvere equazioni differenziali. Come per la lezione della volta scorsa, mostro qui qual è il risultato atteso per gli esercizi, usando Julia.

Iterare sui tempi

In tutti gli esercizi di oggi si richiede di iterare sul tempo $t$, perché la soluzione numerica delle equazioni differenziali richiede di partire dalla condizione iniziale al tempo $t = t_0$ e procedere a incrementi di $h$ finché non si raggiunge il tempo finale $t_f$:

std::array<double, 2> x{...};  // Condizione iniziale
while (...) {
    // Sovrascrive "x" al tempo t con "x" al tempo t + h
    x = myRK.Passo(t, x, h);
    t += h;
}

È importante scrivere bene la condizione nel ciclo while, perché è una cosa che gli studenti sbagliano spesso! Il problema sta negli errori di arrotondamento, che sono dovuti al modo in cui il computer memorizza i numeri floating-point e sono quindi identici sia in C++ che in Julia.

Vediamo quindi in cosa consiste il problema usando Julia. Creiamo una variabile t = 0 che poi incrementiamo in passi di h = 0.1 secondi: in questo modo simuliamo quello che farebbe il ciclo per risolvere una equazione differenziale

t = 0
h = 0.1
t += h

0.1

Nulla di sorprendente… Incrementiamo ancora un paio di volte:

t += h
t += h

0.30000000000000004

Sorpresa! Con tre incrementi si è rivelato un piccolo errore di arrotondamento che era nascosto già nel primo passaggio. Il problema è che il numero 0.1 con cui incrementavamo ogni volta la variabile t non è rappresentabile nel formato floating-point usato dai calcolatori moderni, che usano lo standard IEE 754; di conseguenza, il computer è stato costretto a scrivere nella variabile h una approssimazione del valore 0.1:

$$h = 0.1 + \varepsilon.$$

Quando si sommano $N$ valori di $h$, si ottiene quindi il risultato

$$\sum_{i=1}^N h = N\times 0.1 + N \times \varepsilon.$$

L'errore si accumula, passaggio dopo passaggio, diventando visibile nel nostro esempio solo al terzo passaggio ($N = 3$).

Considerate ora un codice come questo, che vorrebbe iterare per t che va da 0 a 1 in step di h = 0.1:

function simulate(t0, tf, h)
    t = t0

    println("Inizia la simulazione, da t=$t0 a $tf con h=$h")

    # Itera finché non abbiamo raggiunto il tempo finale
    while t < tf
        println("  t = $t")
        t += h
    end

    println("Simulazione terminata a t = $t")
end

simulate(0.0, 1.0, 0.1)

Inizia la simulazione, da t=0.0 a 1.0 con h=0.1
  t = 0.0
  t = 0.1
  t = 0.2
  t = 0.30000000000000004
  t = 0.4
  t = 0.5
  t = 0.6
  t = 0.7
  t = 0.7999999999999999
  t = 0.8999999999999999
  t = 0.9999999999999999
Simulazione terminata a t = 1.0999999999999999

Il codice si è arrestato al tempo $t \approx 1.1$ anziché al tempo $t = 1$! Questa implementazione di while è molto comune nei compiti scritti dei vostri colleghi degli anni scorsi, ma è ovviamente sbagliata. Il modo giusto per implementare questo genere di ciclo è di calcolare il numero di iterazioni (come un intero) e poi fare un ciclo for usando solo variabili intere; ovviamente il numero di iterazioni $N$ è dato da

$$N = \frac{t_f - t_0}h.$$

Definiamo quindi una funzione che, dati i tempi iniziale e finale e il passo $h$, determina il numero di passi:

num_of_steps(t0, tf, h) = round(Int, (tf - t0) / h)

num_of_steps (generic function with 1 method)

Vediamo che con questa funzione l'iterazione termina correttamente, anche se il valore di t non è esattamente quello atteso:

function simulate_method1(t0, tf, h)
    println("Inizia la simulazione, da t=$t0 a $tf con h=$h")

    # Calcola il numero di iterazioni prima di iniziare il ciclo
    # vero e proprio
    nsteps = num_of_steps(t0, tf, h)
    t = t0
    for i = 1:nsteps
        println("  t = $t")
        # Incrementa come al solito
        t += h
    end
    println("Simulazione terminata a t = $t")
end

simulate_method1(0, 1, 0.1)

Inizia la simulazione, da t=0 a 1 con h=0.1
  t = 0
  t = 0.1
  t = 0.2
  t = 0.30000000000000004
  t = 0.4
  t = 0.5
  t = 0.6
  t = 0.7
  t = 0.7999999999999999
  t = 0.8999999999999999
Simulazione terminata a t = 0.9999999999999999

In questo caso il ciclo si è arrestato al valore $t \approx 1$, con un errore $\delta t \sim 10^{-16}$ che è trascurabile perché è dello stesso ordine di grandezza dell'errore di arrotondamento atteso per una variabile double: l'implementazione quindi è corretta.

Un'alternativa è quella di aggiornare t usando la formula $t_i = t_0 + i \cdot h$:

function simulate_method2(t0, tf, h)
    println("Inizia la simulazione, da t=$t0 a $tf con h=$h")

    # Calcola il numero di iterazioni prima di iniziare il ciclo vero
    # e proprio
    nsteps = num_of_steps(t0, tf, h)
    t = t0
    for i = 1:nsteps
        println("  t = $t")
        # Ricalcola t partendo da t0 e da h, usando il contatore i
        t = t0 + i * h
    end
    println("Simulazione terminata a t = $t")
end

simulate_method2(0, 1, 0.1)

Inizia la simulazione, da t=0 a 1 con h=0.1
  t = 0
  t = 0.1
  t = 0.2
  t = 0.30000000000000004
  t = 0.4
  t = 0.5
  t = 0.6000000000000001
  t = 0.7000000000000001
  t = 0.8
  t = 0.9
Simulazione terminata a t = 1.0

Come vedete, non c'è grande differenza tra i due metodi: entrambi producono piccoli errori di arrotondamento qua e là, ma la precisione complessiva è confrontabile, e soprattutto in nessuno dei due casi l'errore si accumula.

Esercizio 8.0: Algebra vettoriale

Testo dell'esercizio: carminati-esercizi-08.html.

In Julia non è necessario implementare le operazioni aritmetiche su vettori, perché sono già implementate: basta porre un punto . davanti all'operatore perché questo venga automaticamente propagato sugli elementi di vettori:

[1, 2, 4] .+ [3, 7, -5]

3-element Vector{Int64}:
  4
  9
 -1

Questo vale per qualsiasi operatore: -, *, ma anche gli operatori di assegnazione =, di incremento +=, e addirittura di chiamata di funzione:

# Applica la funzione `log10` a tutti gli elementi dell'array
log10.([1, 2, 4])

3-element Vector{Float64}:
 0.0
 0.3010299956639812
 0.6020599913279624

Esercizio 8.1: metodo di Eulero

Testo dell'esercizio: carminati-esercizi-08.html.

In Julia è semplicissimo definire il metodo di Eulero: basta una riga, se si usano gli operatori con il punto!

euler(fn, x, t, h) = x .+ fn(t, x) .* h

euler (generic function with 1 method)

In Julia non c'è bisogno di definire una classe base FunzioneVettorialeBase da cui derivare altre classi come OscillatoreArmonico eccetera: basta passare la funzione nel parametro fn (primo argomento). È un meccanismo simile a quello visto nella lezione precedente usando i template, anche se in Julia la risoluzione dei template avviene a runtime anziché in fase di compilazione come in C++.

Definiamo ora una funzione che descriva l'oscillatore armonico del problema 8.1.

oscillatore(time, x) = [x[2], -x[1]]  # ω0 = 1

oscillatore (generic function with 1 method)

Invochiamo oscillatore usando come condizione iniziale $(x, v) = (0, 1)$. Vediamo che euler restituisce il valore di $(x, v)$ calcolato al tempo $t = 0 + h = h$:

h = 0.1
result = euler(oscillatore, [0., 1.], 0., h)

2-element Vector{Float64}:
 0.1
 1.0

Il risultato ha senso: la posizione aumenta da 0.0 a 0.1, ma la velocità sembra non aumentare perché l'incremento è del secondo ordine (è l'accelerazione a far muovere il corpo!), mentre il metodo di Eulero è del primo ordine, quindi troppo inaccurato per accorgersene dopo un solo step. Se evolviamo ancora una volta, vediamo che finalmente la velocità inizia a diminuire:

# Al posto della condizione iniziale, passiamo `result` (la
# soluzione al tempo t=h), e al posto del tempo 0.0 passiamo
# il tempo 0.0+h
result = euler(oscillatore, result, 0. + h, h)

2-element Vector{Float64}:
 0.2
 0.99

Definiamo ora una variabile che contenga il tempo finale a cui la nostra simulazione deve arrestarsi:

lastt = 70.0;

Per iterare euler, possiamo scrivere una funzione che salva tempo, posizione e velocità in un vettore e lo restituisce. Questa funzione richiede come parametri la condizione iniziale $\vec x_0$, il tempo iniziale $t_0$ e finale $t_f$, e il passo $h$, e restituisce tre vettori:

1. Un vettore di tempi

2. Un vettore di posizioni

3. Un vettore di velocità

function euler_simulation(x0, t0, tf, h)
    # Calcola il numero di iterazioni prima di iniziare il ciclo vero
    # e proprio
    nsteps = num_of_steps(t0, tf, h)

    # I tre vettori hanno `N + 1` elementi e non `N`, perché vogliamo
    # memorizzare anche la condizione iniziale.
    times = zeros(Float64, nsteps + 1)
    pos = zeros(Float64, nsteps + 1)
    vel = zeros(Float64, nsteps + 1)

    # Salviamo la condizione iniziale
    times[1] = t0
    pos[1] = x0[1]
    vel[1] = x0[2]

    t = t0
    x = x0
    for i = 1:nsteps
        x = euler(oscillatore, x, t, h)
        t += h

        times[i + 1] = t
        pos[i + 1] = x[1]
        vel[i + 1] = x[2]
    end

    # Contrariamente al C++, una funzione Julia può restituire
    # più di un valore
    return (times, pos, vel)
end

times, pos, vel = euler_simulation([0.0, 1.0], 0.0, lastt, 0.1);

Nel vostro codice C++ non è necessario inventarsi chissà quali metodi per restituire più di un valore (anche se in C++ è possibile, usando ad esempio std::tuple): potete semplicemente stampare i valori di $t_i$, $x_i$ e $v_i$ man mano che li calcolate dentro il ciclo for, oppure aggiungendoli a un punto di un grafico Gnuplot o ROOT.

Stampiamo a video i primi valori, per controllare che siano plausibili:

using Printf

for i in 1:5
    @printf("%.2f\t%f\t%f\n", times[i], pos[i], vel[i])
end

0.00	0.000000	1.000000
0.10	0.100000	1.000000
0.20	0.200000	0.990000
0.30	0.299000	0.970000
0.40	0.396000	0.940100

E stampiamo anche gli ultimi:

for i in (length(times) - 5):length(times)
    @printf("%.2f\t%f\t%f\n", times[i], pos[i], vel[i])
end

69.50	4.890629	31.366165
69.60	8.027245	30.877102
69.70	11.114956	30.074378
69.80	14.122393	28.962882
69.90	17.018682	27.550643
70.00	19.773746	25.848775

Numeri per test in C++

Potete usare questi valori per scrivere una funzione C++ che verifichi l'implementazione con degli assert.

Nello stabilire il passo di integrazione occorre fare un'osservazione molto importante: se vogliamo paragonare la soluzione calcolata da euler, possiamo semplicemente paragonare l'ultimo valore di pos.GetComponente(0) col valore $\sin(70)$. Ma questo funziona se effettivamente il valore della variabile $t$ durante l'ultima iterazione del ciclo for è uguale a 70, e questo vale solo se $\Delta t = 70\,\text{s}$ è esattamente divisibile per $h$.

Chiarisco il problema con un esempio: se devo fare una simulazione da $t_0 = 0\,\text{s}$ fino a $t_f = 5\,\text{s}$, ma uso il passo $h = 2\,\text{s}$, non raggiungerò mai il valore di $t_f$, perché la sequenza dei tempi sarà 0, 2, 4, 6, …, e non potrò conoscere quindi il valore della soluzione al tempo $t = 5\,\text{s}$.

Non scegliete quindi a caso i valori di $h$, ma definiteli sempre in funzione del numero di passi che volete far compiere. Il modo più sicuro, ancora una volta, è di definire prima il numero $N$ di passi, e poi stabilire il valore di $h$ dalla formula

$$h = \frac{t_f - t_0}N.$$

(Ho scritto: “ancora una volta”, perché questo suggerimento segue la medesima filosofia che ci aveva fatto definire la funzione num_of_steps sopra, quando avevamo detto che è meglio stabilire il numero di passi in anticipo per evitare di simulare uno step in più o in meno).

Nel codice Julia faremo esattamente così: definiamo un vettore di valori di $N$, chiamato nsteps, usando la formula $7\times 10^k$, con $k \in [2, 2.2, 2.4, 2.6, \ldots, 3.8, 4]$: in questo modo i valori di $N$ agli estremi sono 700 e 70000, che portano ad $h = 10^{-1}$ e $h = 10^{-3}$. Il valore di nsteps deve ovviamente essere sempre arrotondato ad un intero (mediante round).

nsteps = 7 * round.(Int, exp10.(2:0.2:4))

11-element Vector{Int64}:
   700
  1106
  1757
  2786
  4417
  7000
 11095
 17584
 27867
 44170
 70000

In deltat memorizziamo invece i passi temporali (ossia, i valori di $h$) che studieremo più sotto. Come spiegato per l'esercizio 8.0, in Julia l'operatore ./ è come l'operatore / di divisione, ma viene applicato uno ad uno ad ogni elemento dell'array, e risparmia la noia di dover implementare un ciclo for.

deltat = lastt ./ nsteps

11-element Vector{Float64}:
 0.1
 0.06329113924050633
 0.0398406374501992
 0.02512562814070352
 0.01584786053882726
 0.01
 0.006309148264984227
 0.003980891719745223
 0.0025119316754584277
 0.001584786053882726
 0.001

Creiamo ora un'animazione che confronti la soluzione analitica esatta $f(x) = \sin x$ con la soluzione calcolata col metodo euler. In Julia è semplicissimo creare animazioni: basta usare la macro @animate del pacchetto Plots, e poi salvare il risultato in un file GIF.

using Plots

anim = @animate for h in deltat
    (time, pos, vel) = euler_simulation([0.0, 1.0], 0.0, lastt, h)
    plot(time, pos,
         title = @sprintf("h = %.5f", h),
         label="Eulero", ylim=(-2, 2),
         xlabel="Tempo [s]", ylabel="Posizione [m]")
    plot!(time, sin.(time), label = "Risultato atteso")
end

gif(anim, joinpath(@OUTPUT, "euler.gif"), fps = 1);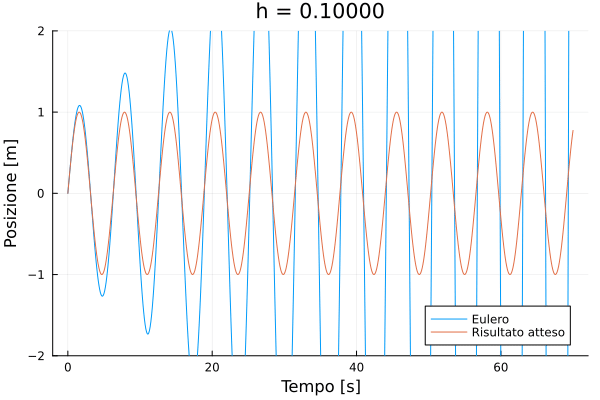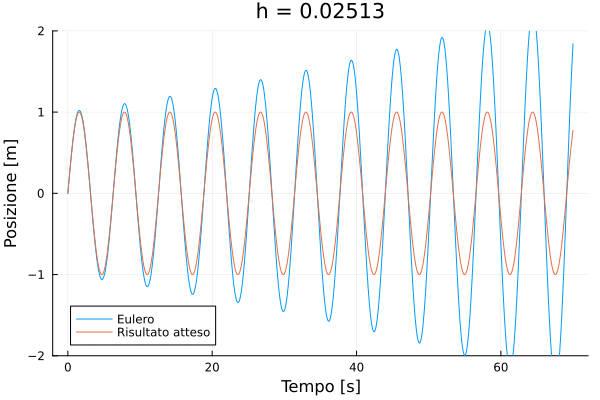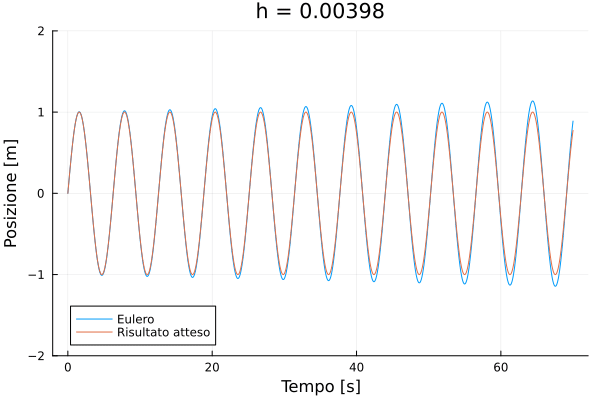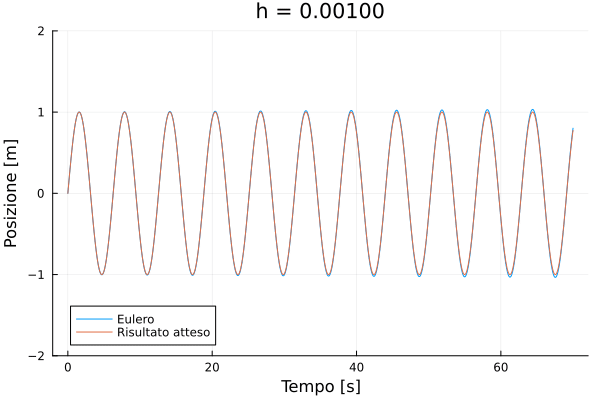

Vediamo che l'errore è estremamente significativo se $h = 10^{-2}$. Facciamo un confronto più quantitativo confrontando il valore della posizione all'istante $t=70\,\text{s}$ con quello teorico.

lastpos = [euler_simulation([0.0, 1.0], 0, lastt, h)[2][end] for h in deltat]
error_euler = abs.(lastpos .- sin(lastt))

@printf("%-14s\t%-14s%-14s\n", "δt [s]", "x(t = 70 s) [m]", "x vero [m]")
for i in 1:length(deltat)
    @printf("%.12f\t%.12f\t%.12f\n", deltat[i], lastpos[i], sin(lastt))
end

δt [s]        	x(t = 70 s) [m]x vero [m]    
0.100000000000	19.773746013860	0.773890681558
0.063291139241	6.491353718714	0.773890681558
0.039840637450	3.020870585603	0.773890681558
0.025125628141	1.841466606636	0.773890681558
0.015847860539	1.341055498792	0.773890681558
0.010000000000	1.096084090818	0.773890681558
0.006309148265	0.964380218087	0.773890681558
0.003980891720	0.889320788243	0.773890681558
0.002511931675	0.844907752921	0.773890681558
0.001584786054	0.817989996041	0.773890681558
0.001000000000	0.801441124227	0.773890681558

I numeri sopra vi saranno preziosi per fare test sul vostro codice usando assert. Creiamo ora un plot che mostri l'andamento dell'errore in funzione del passo $h$, come mostrato sul sito.

plot(deltat, error_euler,
     xscale = :log10, yscale = :log10,
     xlabel = "Passo d'integrazione",
     ylabel = @sprintf("Errore a t = %.1f", lastt),
     label = "");
scatter!(deltat, error_euler, label = "");

Esercizio 8.2: Soluzione con Runge-Kutta

Testo dell'esercizio: carminati-esercizi-08.html.

La funzione rungekutta implementa l'integrazione di Runge-Kutta usando lo stesso approccio della funzione euler vista sopra.

function rungekutta(fn, x, t, h)
    k1 = fn(t, x)
    k2 = fn(t + h / 2.0, x .+ k1 .* h / 2.0)
    k3 = fn(t + h / 2.0, x .+ k2 .* h / 2.0)
    k4 = fn(t + h, x .+ k3 .* h)

    x .+ (k1 .+ 2k2 .+ 2k3 .+ k4) .* h / 6
end

rungekutta (generic function with 1 method)

Dovremmo ora implementare una funzione rk_simulation che, analogamente a quanto avevamo fatto per euler_simulation sopra, iteri per un numero di passi pari al valore restituito da num_of_steps, ma chiamando stavolta rungekutta. Potremmo fare un copia-e-incolla, ma è più elegante pensare a una funzione più generica, che richieda come parametro di input (in method_fn) anche il metodo risolutivo (Eulero o Runge-Kutta). Già che ci siamo, rendiamo più generica la funzione anche sotto un altro aspetto: invece di aspettarci di usare oscillatore come funzione che descrive l'equazione differenziale da risolvere, accettiamola nel nuovo argomento problem_fn. Ecco quindi la funzione eqdiff_simulation, versione più generale di euler_simulation:

function eqdiff_simulation(method_fn, problem_fn, x0, t0, tf, h)
    nsteps = num_of_steps(t0, tf, h)

    times = zeros(Float64, nsteps + 1)
    pos = zeros(Float64, nsteps + 1)
    vel = zeros(Float64, nsteps + 1)

    times[1] = t0
    pos[1] = x0[1]
    vel[1] = x0[2]

    t = t0
    x = x0
    for i = 1:nsteps
        x = method_fn(problem_fn, x, t, h)
        t += h

        times[i + 1] = t
        pos[i + 1] = x[1]
        vel[i + 1] = x[2]
    end

    return (times, pos, vel)
end

eqdiff_simulation (generic function with 1 method)

Verifichiamo che produca gli stessi risultati di euler_simulation:

(time_euler, pos_euler, vel_euler) = euler_simulation(
    [0.0, 1.0],
    0.0,
    lastt,
    h,
);
(time_eqdiff, pos_eqdiff, vel_eqdiff) = eqdiff_simulation(
    euler,
    oscillatore,
    [0.0, 1.0],
    0.0,
    lastt,
    h,
);

Calcoliamo ora il valore assoluto della differenza delle posizioni (farlo sulle velocità sarebbe lo stesso), e stampiamo il coefficiente più grande:

maximum(abs.(pos_euler .- pos_eqdiff))

0.0

Il risultato è 0.0, il che vuol dire che le posizioni ottenute con i due metodi sono uguali: ottimo!

Risolviamo ora il problema dell'oscillatore con Runge-Kutta:

(time, pos, vel) = eqdiff_simulation(
    rungekutta,
    oscillatore,
    [0., 1.],
    0.0,
    70.0,
    0.1,
);

Come sopra, consideriamo visualizziamo i tempi, le posizioni e le velocità all'inizio della simulazione:

using Printf

for i in 1:5
    @printf("%.2f\t%f\t%f\n", times[i], pos[i], vel[i])
end

0.00	0.000000	1.000000
0.10	0.099833	0.995004
0.20	0.198669	0.980067
0.30	0.295520	0.955337
0.40	0.389418	0.921061

Questi sono i dati alla fine della simulazione:

for i in (length(times) - 5):length(times)
    @printf("%.2f\t%f\t%f\n", times[i], pos[i], vel[i])
end

69.50	0.375468	0.926830
69.60	0.466121	0.884716
69.70	0.552116	0.833761
69.80	0.632595	0.774476
69.90	0.706754	0.707453
70.00	0.773850	0.633361

Numeri per test in C++

Potete usare questi valori per scrivere una funzione C++ che verifichi l'implementazione con degli assert.

Nel caso di Runge-Kutta, l'animazione è molto meno interessante: la convergenza è eccellente anche per $h = 10^{-1}$.

anim = @animate for h in deltat
    cur_result = eqdiff_simulation(
        rungekutta,
        oscillatore,
        [0., 1.],
        0.0,
        70.0,
        h,
    )
    plot(times, pos,
         title = @sprintf("h = %.5f", h),
         label="Eulero", ylim=(-2, 2),
         xlabel="Tempo [s]", ylabel="Posizione [m]")
    plot!(times, sin.(times), label = "Risultato atteso")
end

gif(anim, joinpath(@OUTPUT, "rk.gif"), fps = 1);

Confrontiamo il grafico dell'errore di Runge-Kutta con quello di Eulero, per rendere evidente la differenza nella velocità di convergenza.

lastpos = [
    eqdiff_simulation(
        rungekutta,
        oscillatore,
        [0., 1.],
        0.0,
        lastt,
        h,
    )[2][end] for h in deltat
]
error_rk = abs.(lastpos .- sin(lastt))

11-element Vector{Float64}:
 4.0570150020236007e-5
 6.301458916779801e-6
 9.680016646029799e-7
 1.5096724137464435e-7
 2.3677510618824726e-8
 3.7318509393813315e-9
 5.891128695978409e-10
 9.315614946103778e-11
 1.4744427900836854e-11
 2.3335777754596165e-12
 3.597122599785507e-13

Questa è la corrispondenza tra $\delta t$ e la posizione finale (a $t = 70\,\text{s}$):

@printf("%-14s\t%-14s\t%-14s\n", "δt [s]", "x(t = 70 s) [m]", "x vero [m]")
for i in 1:length(deltat)
    @printf("%.12f\t%.12f\t%.12f\n", deltat[i], lastpos[i], sin(lastt))
end

δt [s]        	x(t = 70 s) [m]	x vero [m]    
0.100000000000	0.773850111408	0.773890681558
0.063291139241	0.773884380099	0.773890681558
0.039840637450	0.773889713556	0.773890681558
0.025125628141	0.773890530591	0.773890681558
0.015847860539	0.773890657880	0.773890681558
0.010000000000	0.773890677826	0.773890681558
0.006309148265	0.773890680969	0.773890681558
0.003980891720	0.773890681465	0.773890681558
0.002511931675	0.773890681543	0.773890681558
0.001584786054	0.773890681556	0.773890681558
0.001000000000	0.773890681558	0.773890681558

Creiamo un plot che mostri visivamente la differenza tra i due metodi:

plot(deltat, error_euler, label = "");
scatter!(deltat, error_euler, label = "Eulero");

plot!(deltat, error_rk,
     xscale = :log10, yscale = :log10,
     xlabel = "Passo d'integrazione",
     ylabel = @sprintf("Errore a t = %.1f", lastt),
     label = "");
scatter!(deltat, error_rk, label = "Runge-Kutta");

Dovrebbe esservi ovvio che è sempre meglio preferire il metodo di Runge-Kutta a quello di Eulero (a meno che, ovviamente, un esercizio non vi chieda espressamente di usare il metodo di Eulero!).

Esercizio 8.3

Testo dell'esercizio: carminati-esercizi-08.html.

Questo esercizio richiede di studiare il comportamento di un pendolo di lunghezza $l$ sottoposto ad un'accelerazione di gravità $g$. Impostiamo un paio di costanti.

rodlength = 1.;
g = 9.81;

La funzione pendulum definisce i due membri dell'equazione differenziale di secondo grado.

pendulum(t, x) = [x[2], -g / rodlength * sin(x[1])]

pendulum (generic function with 1 method)

Prima di effettuare lo studio richiesto dall'esercizio, è buona norma studiare il comportamento della soluzione in un caso particolare. Usiamo rungekutta per analizzare il caso in cui $\theta_0 = \pi / 3$:

times, pos, vel = eqdiff_simulation(
    rungekutta,
    pendulum,
    [π / 3, 0.],
    0.0,
    3.0,
    0.01,
)

using Printf

for i in 1:5
    @printf("%.2f\t%f\t%f\n", times[i], pos[i], vel[i])
end

0.00	1.047198	0.000000
0.01	1.046773	-0.084950
0.02	1.045499	-0.169859
0.03	1.043376	-0.254683
0.04	1.040405	-0.339382

Vedete che la velocità angolare diventa subito negativa: ciò è corretto, se pensate al fatto che la condizione iniziale specifica che il pendolo parta da fermo con un angolo positivo. Visualizziamo come al solito anche le ultime righe:

for i in (length(times) - 5):length(times)
    @printf("%.2f\t%f\t%f\n", times[i], pos[i], vel[i])
end

2.95	-0.727354	-2.201111
2.96	-0.749036	-2.135092
2.97	-0.770051	-2.067538
2.98	-0.790382	-1.998529
2.99	-0.810017	-1.928140
3.00	-0.828941	-1.856446

È interessante studiare il pendolo creando un'animazione. Noi useremo il pacchetto Luxor, che consente di creare disegni ed animazioni partendo da forme geometriche primitive. (Se volete creare qualcosa del genere in C++, potete usare la libreria Monet, convertendo poi i file SVG generati da Monet in format PNG con l'interfaccia a linea di comando di Inkscape e assemblando i file PNG in un'animazione MP4 o MKV con ffmpeg).

Per installare Luxor da Internet, usate come al solito i comandi di Pkg:

using Pkg
Pkg.add("Luxor")

Quando è installato, possiamo importarlo come al solito:

import Luxor

In Luxor occorre specificare le dimensioni della superficie su cui si disegna; noi sceglieremo una dimensione di 500×500. Il sistema di coordinate ha origine sempre nel centro dell'immagine, in modo che l'intervallo di valori sugli assi $x$ ed $y$ sarà nel nostro caso $-250\ldots 250$.

La funzione plot_pendulum rappresenta il pendolo come una linea che parte dal centro e alla cui estremità è disegnato un cerchio pieno di colore nero. (Notate che Julia offre il comando sincos, che calcola simultaneamente il valore del seno e del coseno di un angolo).

function plot_pendulum(angle)
    radius = 200  # Lunghezza del braccio del pendolo
    y, x = radius .* sincos(π / 2 + angle)

    Luxor.sethue("black")
    Luxor.line(Luxor.Point(0, 0), Luxor.Point(x, y), :stroke)
    Luxor.circle(Luxor.Point(x, y), 10, :fill)
end

plot_pendulum (generic function with 1 method)

Abbiamo già calcolato la soluzione dell'equazione in un caso particolare, e il risultato è nella matrice oscillations. Il comando size restituisce le dimensioni di vettori, matrici e tensori. Nel caso di oscillations ci sono ovviamente 3 colonne, ma il numero di righe (corrispondente agli step temporali) dipende dal passo $h$ e dalla lunghezza della simulazione. Vediamo di quanti step si tratta:

size(times, 1)

301

Creeremo ora un'immagine GIF animata chiamando ripetutamente il comando plot_pendulum. Notate la comodità di Luxor: in poche righe è possibile creare un'intera animazione e salvarla su disco.

anim = Luxor.Movie(500, 500, "Pendulum")

function animframe(scene, framenumber)
    Luxor.background("white")
    plot_pendulum(pos[framenumber])
end

Luxor.animate(anim, [Luxor.Scene(anim, animframe, 1:size(times, 1))],
    creategif=true, pathname=joinpath(@OUTPUT, "pendulum.gif"));

Adesso che abbiamo visto che l'equazione del pendolo viene integrata correttamente, dobbiamo passare al calcolo del periodo di oscillazione. Come suggerito sul sito, bisogna considerare il momento in cui la velocità angolare inverte il segno. Osserviamo allora il grafico della velocità (seconda componente del sistema di equazioni differenziali).

plot(times, pos,
     label = "",
     xlabel = "Tempo [s]",
     ylabel = "Velocità angolare [rad/s]");

Come già detto sopra per l'esercizio 8.0, nel vostro codice C++ non è necessario che salviate la soluzione in tre array times, pos e vel. Dal momento che l'esercizio richiede di calcolare il periodo del pendolo, che dipende dal momento in cui avviene l'inversione, possiamo scrivere un ciclo while costruito ad hoc per questo caso. Il procedimento che seguiremo è il seguente:

1. Facciamo partire la simulazione; essendo la condizione iniziale $(\theta = \theta_0, \omega = 0)$, il pendolo inizierà a muoversi con velocità angolare $\omega$ negativa.

2. Continuiamo a far procedere la simulazione, finché non vediamo che il segno di $\omega$ diventa positivo: a questo punto siamo certi che un periodo sia stato completato, e il pendolo sta iniziando a tornare indietro verso angoli positivi.

3. Siccome abbiamo arrestato il ciclo quando $\omega > 0$, il tempo passato è un po' più di un semiperiodo: infatti il semiperiodo si ha nel momento esatto in cui $\omega = 0$. Dobbiamo quindi sottrarre dal tempo $t$ una certa quantità. Per stimare questa quantità, possiamo fare una interpolazione lineare tra la velocità all'istante $t - h$, quando ancora $\omega < 0$, e il valore attuale di $t$, in cui abbiamo visto che per la prima volta $\omega > 0$. Scriviamo quindi la retta $\omega = m t + q$ passante per $(t - h, \omega_{i-1})$ e per $(t, \omega_i)$ e imponiamo che $\omega = 0$, ricavando t. Si tratta di un semplice problema di geometria analitica, e la soluzione è la seguente:

$$t(\omega) = t - h + \frac{h}{\omega_{i - 1} - \omega_i}\bigl(\omega_{i - 1} - \omega\bigr).$$

È facile convincersi della correttezza del risultato, perché l'espressione è chiaramente una retta, e vale che agli estremi $t(\omega_{i - 1}) = t - h$ e $t(\omega_i) = \omega_i$.

Nel nostro caso bisogna quindi implementare il calcolo della formula nel caso in cui $\omega = 0$, e raddoppiare il risultato: lo facciamo nella funzione period, che accetta come parametro la matrice a tre colonne prodotta da eqdiff_simulation, e che sfrutta la funzione invtime che fornisce il valore del tempo all'istante della inversione. Implementiamo una serie di sotto-funzioni, in modo che sia più facile verificare il comportamento di ciascuna. Implementiamo una funzione interp che interpoli tra due coppie di punti a $(t_A, \omega_A)$ e b $(t_B, \omega_B)$, dato un certo valore di ω:

interp(a, b, ω) = a[1] - (a[1] - b[1]) / (a[2] - b[2]) * (a[2] - ω)

interp (generic function with 1 method)

Usiamo l'overloading per definire una versione più specifica, che calcola il valore dell'interpolazione nel caso $\omega = 0$.

interp(a, b) = interp(a, b, 0)

interp (generic function with 2 methods)

Eseguiamo una volta interp per trovare il valore dell'ordinata $y$ in corrispondenza dell'ordinata $y = 0.3$ di una una retta passante per i punti $(-0.4, -0.7)$ e $(0.5, 0.8)$:

let p1x = -0.4, p1y = -0.7, p2x = 0.5, p2y = 0.8, y = 0.3
    # Il comando `plot` richiede di passare un array con le ascisse
    # e uno con le coordinate…
    plot([p1x, p2x], [p1y, p2y], label = "");
    # …mentre la nostra `interp` richiede due coppie (x, y)
    let x = interp([p1x, p1y], [p2x, p2y], y)
        @printf("La retta interpolante passa per (%.1f, %.1f)\n", x, y)
        # Il comando `scatter` funziona come `plot`
        scatter!([p1x, x, p2x], [p1y, y, p2y], label = "");
    end
end;

La retta interpolante passa per (0.2, 0.3)

Il grafico mostra che la nostra implementazione di interp funziona a dovere; voi potreste implementare un test nel vostro esercizio:

void test_interp() {
  const double p1x = -0.4, p1y = -0.7;
  const double p2x = 0.5, p2y = 0.8;

  assert(are_close(interp(p1x, p1y, p2x, p2y, 0.3), 0.2));
}

Ora possiamo implementare il codice che calcola il periodo

function period(θ₀; h = 0.01)
    # Simuliamo finché ω non diventa negativa

    x = [θ₀, 0.]
    oldx = [0., 0.]
    t = 0.0
    while x[2] ≤ 0
        oldx = x  # Ci serve poi per fare l'interpolazione
        x = rungekutta(pendulum, x, t, h)
        t += h
    end

    # A questo punto, t è un po' più di un semiperiodo.

    # Calcoliamo mediante interpolazione l'istante in cui
    # si è avuto ω=0
    t_semip = interp((t - h, oldx[2]), (t, x[2]))

    # Il periodo è due volte il semiperiodo
    return 2t_semip
end

period (generic function with 1 method)

Confrontiamola col periodo ideale di un pendolo sottoposto a piccole oscillazioni.

ideal_period = 2π / √(g / rodlength)

2.006066680710647

Creiamo ora il grafico analogo a quello riportato nel testo dell'esercizio.

angles = 0.1:0.1:3.0
ampl = [period(angle) for angle in angles]

@printf("%14s\t%-14s\n", "Angolo [rad]", "Periodo [s]")
for i in eachindex(angles)
    @printf("%14.1f\t%.7f\n", angles[i], ampl[i])
end

plot(angles, ampl, label="", xlabel="Angolo [rad]", ylabel="Periodo [s]");
scatter!(angles, ampl, label="");

  Angolo [rad]	Periodo [s]   
           0.1	2.0073214
           0.2	2.0110933
           0.3	2.0174091
           0.4	2.0263134
           0.5	2.0378677
           0.6	2.0521566
           0.7	2.0692847
           0.8	2.0893812
           0.9	2.1126028
           1.0	2.1391375
           1.1	2.1692090
           1.2	2.2030827
           1.3	2.2410742
           1.4	2.2835593
           1.5	2.3309868
           1.6	2.3838961
           1.7	2.4429402
           1.8	2.5089176
           1.9	2.5828151
           2.0	2.6658708
           2.1	2.7596635
           2.2	2.8662475
           2.3	2.9883659
           2.4	3.1297934
           2.5	3.2959325
           2.6	3.4949131
           2.7	3.7398272
           2.8	4.0538680
           2.9	4.4845820
           3.0	5.1580670

Esercizio 8.4

Testo dell'esercizio: carminati-esercizi-08.html.

Come sopra, definiamo i parametri numerici del problema.

ω0 = 10;
α = 1.0 / 30;
endt = 600.0;

Definiamo anche la funzione che caratterizza l'equazione differenziale. Notate che in questo esercizio, per la prima volta, la funzione dipende esplicitamente dalla variabile time, ossia il tempo $t$:

forcedpendulum(time, x, ω) = [
    x[2],
    -ω0^2 * x[1] - α * x[2] + sin(ω * time),
]

forcedpendulum (generic function with 1 method)

Prima di costruire la simulzione, produciamo un grafico usando la funzione eqdiff_simulation definita sopra per capire il comportamento della soluzione. Il plot mostra come il pendolo forzato con smorzante arrivi presto ad una situazione di equilibrio:

# Usiamo `_` per indicare che non ci interessa salvare la velocità
# in una variabile, e usiamo una funzione “lambda”
(time, pos, _) = eqdiff_simulation(
    rungekutta,
    (time, x) -> forcedpendulum(time, x, 8.0),
    [0., 0.],
    0.,
    endt,
    0.1,
)

plot(time, pos, label="", xlabel="Tempo [s]", ylabel="Posizione [m]");

Rispetto all'esercizio precedente, dobbiamo calcolare qui non il periodo bensì l'ampiezza di oscillazione (che nell'esercizio precedente era fissata dalla condizione iniziale). Come prima, anche qui non possiamo avere la garanzia che l'integrazione con RK passerà dall'istante in cui il valore della velocità si annulla esattamente, e dovremo quindi usare di nuovo la funzione interp. Il modo migliore di procedere è quindi il seguente:

1. Iteriamo RK per un tempo ragionevole in modo da toglierci dalla regione iniziale di instabilità; nell'esempio sotto, il codice Julia integra fino al tempo $15/\alpha$;

2. A questo punto il codice cerca nuovamente una inversione nel segno della velocità;

3. Trovata l'inversione, sappiamo che il massimo avviene in qualche istante che sta tra $t$ e $t + h$. Troviamo questo istante $t_\text{inv}$ con una interpolazione lineare tra il punto $(t, \omega_0)$ e $(t + h, \omega_1)$

4. Eseguiamo di nuovo RK partendo dal tempo $t$, ma questa volta non usiamo come incremento $h$ bensì $t_\text{inv} - t$. (Alternativamente, si può partire da dove si è arrivati e fare uno step con passo negativo $h = t - t_\text{inv} < 0$: infatti sia il metodo di Eulero che il Runge-Kutta funzionano in entrambe le direzioni temporali!)

5. Se abbiamo fatto le cose per bene, dopo una singola esecuzione di RK ci troviamo in corrispondenza del massimo. (Suggerimento per il debug: se stampate con cerr il secondo elemento dell'array x, la velocità, dovreste ottenere un numero pressoché nullo).

6. Se effettivamente la velocità è praticamente nulla (diciamo $\left|v\right| \leq 10^{-6}\,\text{rad/s}$, il valore della posizione in questo punto corrisponde all'ampiezza.

function forced_pendulum_amplitude(ω)
    # In Julia posso assegnare a una variabile la definizione di una
    # funzione!
    fn = (time, x) -> forcedpendulum(time, x, ω)

    # Step 1: lascio che la simulazione proceda finché l'oscillatore
    # non si stabilizza

    x = [0., 0.]
    t = 0.0

    while t < 15 / α
        x = rungekutta(fn, x, t, h)
        t += h
    end

    # Step 2: continuo a simulare finché il segno della velocità non
    # si inverte

    oldx = [0., 0.]
    while true
        oldx = x
        x = rungekutta(fn, x, t, h)
        t += h

        if x[2] * oldx[2] < 0
            break
        end
    end

    # Step 3: eseguo una interpolazione per sapere di quanto
    # “arretrare” col tempo. Dovrà essere per forza h_new < 0

    h_new = interp((-h, oldx[2]), (0, x[2]))
    @assert h_new < 0

    x = rungekutta(fn, x, t, h_new)

    # Devo usare `abs`: non so a priori se l'oscillatore è a destra o
    # a sinistra dello zero
    return abs(x[1])
end

forced_pendulum_amplitude (generic function with 1 method)

Chiamiamo la funzione forced_pendulum_amplitude su un caso specifico: questo è un numero buono per essere usato in un assert. Notate che nel secondo punto (corrispondente al tempo $t + \delta t$) la velocità è nulla.

forced_pendulum_amplitude(9.5)

0.11236885617836574

Ricreiamo ora il grafico presente sul sito del corso. Usate alcuni dei numeri scritti qui sotto per verificare che il vostro codice sia corretto.

# Aggiungiamo 0.01 agli estremi (9 e 11) per evitare la condizione di risonanza
freq = 9.01:0.05:11.01
ampl = [forced_pendulum_amplitude(ω) for ω in freq]

@printf("%14s\t%-14s\n", "ω [Hz]", "Ampiezza [m]")
for i in eachindex(freq)
    @printf("%14.2f\t%.9f\n", freq[i], ampl[i])
end

plot(freq, ampl,
     label="", xlabel="Frequenza [rad/s]", ylabel="Ampiezza");
scatter!(freq, ampl, label="");

        ω [Hz]	Ampiezza [m]  
          9.01	0.055312613
          9.06	0.058435677
          9.11	0.061433676
          9.16	0.065428108
          9.21	0.069135823
          9.26	0.074439247
          9.31	0.079902022
          9.36	0.086671352
          9.41	0.093976526
          9.46	0.103591678
          9.51	0.114312060
          9.56	0.128937200
          9.61	0.146182223
          9.66	0.171004463
          9.71	0.203120780
          9.76	0.251098643
          9.81	0.322386463
          9.86	0.434542823
          9.91	0.584133830
          9.96	0.622486846
         10.01	0.481652699
         10.06	0.348215723
         10.11	0.267258002
         10.16	0.212047762
         10.21	0.176149356
         10.26	0.149165720
         10.31	0.129889992
         10.36	0.114188764
         10.41	0.102407357
         10.46	0.092186372
         10.51	0.083201619
         10.56	0.077112541
         10.61	0.070596611
         10.66	0.066167676
         10.71	0.061280364
         10.76	0.057869529
         10.81	0.054092215
         10.86	0.051333712
         10.91	0.048215540
         10.96	0.046101042
         11.01	0.043584425