Esercizi per oggi

[La pagina con la spiegazione originale degli esercizi si trova qui: https://labtnds.docs.cern.ch/Lezione7/Lezione7/.]

In questa lezione implementeremo alcuni algoritmi di quadratura numerica, cioè algoritmi per il calcolo di integrali definiti di funzioni in un intervallo chiuso e limitato. I metodi numerici che studieremo in questa sessione si possono rendere necessari in varie occasioni: quando non sappiamo valutare analiticamente l’integrale in esame, quando la soluzione analitica è molto complicata ed il calcolo numerico è molto più semplice, oppure quando la funzione è conosciuta in un numeri finito di punti.

Esercizio 7.0 - Integrazione con il metodo midpoint a numero di passi fissato

Implementare un codice per il calcolo della funzione x \sin(x) su [0, \pi/2] con il metodo midpoint.

Per prima cosa, costruiamo un programma di test che calcoli l’integrale utilizzando un numero di intervalli fissato e passato da riga di comando.
Per controllare la precisione ottenuta con un numero di passi fissato, stampiamo una tabella con la differenza tra il risultato numerico ed il valore esatto (ottenuto analiticamente) in funzione del numero di passi (o della lunghezza del passo h). In aggiunta alla tabella si può rappresentare l’andamento dell’errore in funzione della lunghezza del passo h con un grafico, usando gplot++ oppure un TGraph di ROOT.

Il metodo del mid-point

Ricordiamo che in questo metodo l’approssimazione dell’integrale è definita dalla formula

\int_a^b f(x)\,\mathrm{d}x = h \cdot \bigl(f(x_0) + f(x_1) + \ldots + f(x_{N - 1})\bigl), dove h = \frac{b - a}N e x_k = a + \left(k + \frac12 \right) h,\qquad k = 0, 1, \ldots, N - 1.

La formula fornisce un’accuratezza dell’integrale di O(h^2). Notate che questo metodo non richiede il calcolo della funzione negli estremi di integrazione.

Cenni sull’implementazione

L’algoritmo può essere implementato con uno schema del tipo classe madre astratta/classe derivata, che abbiamo già utilizzato nella lezione precedente. Si potrebbe pensare ad una organizzazione di questo tipo:

Prepariamo una classe astratta Integral, che rappresenta un generico algoritmo di integrazione. Il suo costruttore accetta come parametri gli estremi a e b di integrazione, e controlla il loro ordinamento: se a > b, il segno dell’integrale deve essere scambiato.

La classe implementa (tra le varie cose) un metodo virtuale puro

virtual double calculate(int step, const FunzioneBase & f) = 0;

Il metodo calculate è definito come private e non può essere invocato all’esterno della classe. Esso viene invocato dal metodo pubblico (stavolta sì!) integrate, che si preoccupa di verificare gli estremi a e b e li scambia se a > b.
La suddivisione dell’implementazione in calculate (privato) e integrate (pubblico) permette alle classi derivate di assumere nell’implementazione di calculate sempre che a < b, perché se ne occupa il metodo integrate che è sempre lo stesso (non è virtual).
Il metodo midpoint viene concretamente implementato in una classe derivata Midpoint sovrascrivendo il metodo privato calculate.

#pragma once

#include "funzioni.h"
#include <cstdlib>  // Per std::exit()
#include <iostream> // Per std::cerr

using namespace std;

class Integral {
public:
  Integral() : m_a{}, m_b{}, m_sign{}, m_h{} {}

  double integrate(double a, double b, int nstep, FunzioneBase &f) {
    // Questo metodo fa molto poco: imposta `a` e
    // `b`, verifica che a < b, e poi invoca il
    // metodo virtuale `calculate`, che va ridefinito
    // nelle classi derivate
    checkInterval(a, b);
    return m_sign * calculate(nstep, f);
  }

  double getA() const { return m_a; }
  double getB() const { return m_b; }
  double getSign() const { return m_sign; }
  double getH() const { return m_h; }
  void setH(double h) { m_h = h; }

private:
  // Questa è la funzione da ridefinire con `override` nelle classi derivate
  // Essa usa come estremi di integrazione m_a ed m_b, ed è *sempre*
  // garantito che m_a < m_b (perché se ne occupa `Integral::integrate`)
  // (Notate che un metodo si può ridefinire nelle classi derivate anche
  // se è `private`!)
  virtual double calculate(int nstep, FunzioneBase &f) = 0;

  void checkInterval(double a, double b) {
    m_a = std::min(a, b);
    m_b = std::max(a, b);
    m_sign = (a < b) ? 1 : -1;
  }

  double m_a, m_b;
  double m_sign;
  double m_h;
};

// Classe derivata, implementa il metodo mid-point
class Midpoint : public Integral {
public:
  Midpoint() : Integral() {}

private:
  double calculate(int nstep, FunzioneBase &f) override {
    // Ricordare: in quest'implementazione possiamo
    // assumere che m_a < m_b, perché il controllo
    // viene fatto da `Integral::integrate`

    if (nstep < 0) {
        cerr << "Errore, il numero di passi non può essere negativo!\n";
        exit(1);
    }

    m_h = (getB() - getA()) / nstep;
    double sum{};

    for (int i{}; i < nstep; i++) {
      sum += f.Eval(m_a + (i + 0.5) * m_h);
    }

    // Non c'è bisogno di moltiplicare per m_sign,
    // questo verrà fatto dalla funzione (pubblica)
    // `Integral::integrate` della classe primitiva
    return sum * m_h;
  }
};

(Attenzione: il codice sopra ha un problema di accessibilità e non compila. Cercate di capire da soli in che modo sistemarlo, e se non riuscite, chiedete al docente o all’assistente).

Notate in che modo il codice implementa il calcolo: il metodo pubblico è Integral::integrate, che non è virtuale: esso si preoccupa di invocare Integral::checkInterval (privato) per verificare gli estremi di integrazione, e poi invoca il metodo privato Integral::calculate che fa il conto vero e proprio:

double integrate(double a, double b, int nstep, FunzioneBase &f) {
  checkInterval(a, b);
  return m_sign * calculate(nstep, f);
}

In questo modo il metodo calculate può usare gli estremi restituiti da getA()/getB() senza doversi preoccupare del caso a > b. Se vi stupisce che il metodo calculate, pur essendo dichiarato private, possa essere ridefinito nella classe derivata Midpoint, considerate che private indica chi può chiamare il metodo (solo la classe Integrate e non le sue derivate), ma non pone restrizioni su chi possa ridefinirlo.

Viene ora fornito un codice per verificare il funzionamento di quanto implementato finora, che usa la libreria fmtlib. Come al solito, potete installarla usando lo script install_fmt_library: scaricatelo nella directory dell’esercizio ed eseguitelo con sh install_fmt_library, oppure eseguite direttamente questo comando:

In alternativa, scaricate questo file zip nella directory dell’esercizio e decomprimetelo. Le istruzioni dettagliate sono in questa pagina.

Ecco il codice di esempio:

#include "integral.h"
#include "funzioni.h"

#include <cmath>
#include <iostream>
#include <numbers>
#include <string>
#include "fmtlib.h"

using namespace std;

int main (int argc, char* argv[]) {
  if (argc != 2) {
    fmt::println(stderr, "Usage: {} <NSTEP>", argv[0]);
    return 1;
  }

  int nstep{stoi(argv[1])};

  XSinX f{};
  Midpoint myInt{};

  double I{myInt.integrate(0, numbers::pi / 2, nstep, f)};

  fmt::println("Passi: {}, I = {}", nstep, I);
}

dove abbiamo utilizzato una classe XSinX che eredita dalla classe astratta FunzioneBase.

Per creare i grafici, potete ovviamente usare ROOT, oppure gplot++. In quest’ultimo caso, scaricate il file gplot++.h (facendo click col tasto destro sul link) e scrivete un codice del genere:

std::vector<int> steps{10, 50, 100, 500, 1000};
std::vector<double> step_sizes(ssize(steps));
std::vector<double> errors(ssize(steps));

// Calcola gli errori e stampa una tabella usando "fmtlib.h"
double true_value{1};
fmt::println("Passi        Intervallo h  Errore");
for (size_t i{}; i < ssize(steps); ++i) {
  double estimated_value{myInt.integrate(steps[i], f)};
  errors[i] = fabs(estimated_value - true_value);
  step_sizes[i] = myInt.GetH();
  fmt::println("{:12d} {:14.8e} {:20.8e}", steps[i], step_sizes[i], errors[i]);
}

// Crea un plot
Gnuplot plt{};
const std::string output_file_name{"midpoint-error.png"};
plt.redirect_to_png(output_file_name, "800,600");
plt.set_logscale(Gnuplot::AxisScale::LOGXY);
plt.plot(step_sizes, errors);
plt.set_xlabel("Passo di integrazione h");
plt.set_ylabel("Errore");
plt.show();
// È sempre consigliato fornire un messaggio all'utente
// per comunicare che è stato salvato un plot. Includete
// sempre il nome del file nel messaggio!
fmt::println("Plot saved in '{}'", output_file_name);

Con ROOT si scriverebbe invece qualcosa del genere:

std::vector<int> steps{10, 50, 100, 500, 1000};
TGraph g_errore{};
double true_value{1};
fmt::println("Passi        Errore")
for (int i{}; i < size(steps); i++) {
  double estimated_value{myInt.integrate(steps[i], f)};
  double err{fabs(estimated_value - true_value)};
  fmt::println("{:12d} {:20.8e}", steps[i], err);
  g_errore.SetPoint(i, myInt.GetH(), err);
}

E i test?

Da oggi non fornirò più direttamente il codice delle funzioni test_??(). Fornirò però una implementazione completa di ogni esercizio scritta nel linguaggio Julia. È un linguaggio molto semplice da leggere, ma il fatto che sia diverso dal C++ impedirà di “barare” facendo copia-e-incolla dei miei esempi.

Per ogni esercizio, il codice Julia esegue una serie di calcoli che vi forniscono i risultati attesi. Sarà semplice quindi per voi creare da soli le funzioni test_??().

Il notebook Julia per la lezione corrente si trova all’indirizzo https://ziotom78.github.io/tnds-notebooks/lezione07/.

Esercizio 7.1 - Integrazione alla Simpson (da consegnare)

Implementare l’integrazione con il metodo di Simpson con un numero di passi fissato. Si può utilizzare lo stesso schema dell’esercizio precedente costruendo una classe derivata Simpson. Come nell’Esercizio 7.0, stampare una tabella (o costruire un grafico) con la precisione raggiunta in funzione del numero di passi.

Il metodo Simpson

Nel metodo di integrazione alla Simpson, la funzione integranda è approssimata, negli intervalli [x_k, x_{k + 2}] (dove k è un intero pari e x_k = a + k h) con un polinomio di secondo grado i cui nodi sono nei punti \bigl(x_k, f(x_k)\bigr), \bigl(x_{k + 1}, f(x_{k + 1})\bigr), \bigl(x_{k + 2}, f(x_{k + 2})\bigr). Esso fornisce una valutazione dell’integrale con una precisione pari a h^4. La sua applicazione richiede che il numero di passi sia pari e la formula che approssima l’integrale è

\int_a^b f(x)\,\mathrm{d}x = h \cdot \left( \frac13 f(x_o) + \frac43 f(x_1) + \frac23 f(x_2) + \frac43 f(x_3) + \ldots + \frac23 f(x_{N - 2}) + \frac43 f(x_{N - 1}) + \frac13 f(x_N)\bigl) \right),

dove vale che

h = \frac{b - a}N, \quad x_k = a + k h \qquad k = 0, 1, \ldots N.

Test

Come scritto per l’esercizio 7.0, il notebook Julia per la lezione corrente all’indirizzo https://ziotom78.github.io/tnds-notebooks/lezione07/ contiene una serie di risultati che potete usare per scrivere i vostri test.

Esercizio 7.2 - Integrazione con la formula dei trapezi con precisione fissata (da consegnare)

Concludiamo l’esercitazione implementando l’integrazione della funzione x \sin x su [0, \pi] con il metodo dei trapezi. In quest’ultimo esercizio implementiamo un algoritmo di integrazione numerica a precisione fissata invece che a numero di passi fissato. Negli esercizi precedenti il calcolo a numero di passi fissato non ci dà alcuna indicazione sulla qualità del risultato: integrare con 10 passi è sufficiente? L’idea che vogliamo sviluppare è che l’utente fornisca una precisione desiderata e l’algoritmo sia in grado di aumentare automaticamente il numero di passi fino a raggiungere la precisione richiesta sul valore dell’integrale. L’algoritmo dovrà accettare in input il valore della precisione e raddoppiare il numero di passi finché l’errore (stimato runtime, si veda sotto) non diventa inferiore alla precisione impostata.

Come nei casi precedenti si può costruire una classe dedicata per l’implementazione del metodo dei trapezi.

Possiamo implementare come nei casi precedenti un metodo privato

double calculate(int nstep, const FunzioneBase & f) override { ... }

Il punto che ci interessa maggiormente è realizzare un metodo dei trapezi che lavori a precisione fissata. Noi implementeremo il calcolo a precisione fissata solo per il metodo dei trapezi, quindi non toccheremo la classe Integral; di conseguenza, implementeremo solo un metodo integrate_prec in Trapezi:
```
double integrate_prec(double a, double b, double prec, const FunzioneBase & f) { ...
}
```
Ovviamente, è possibile definire una coppia di funzioni integrate_prec (pubblica) e calculate_prec (privata) già nella classe Integral e poi implementare calculate_prec in ogni classe derivata. Bisogna però fare attenzione, perché il calcolo dell’errore dipende dall’ordine dell’algoritmo, quindi sarebbe necessario definire un nuovo metodo astratto calculate_error() che accetti l’integrale calcolato con passo h e con passo h/2 per determinare l’errore corretto, e invocarlo poi in integrate_prec (il metodo pubblico). Noi, come già detto, non faremo nulla di ciò: ci basta implementare l’algoritmo a precisione fissata per il solo metodo dei trapezi. La classe Trapezoids avrà quindi un’implementazione simile:
```
class Trapezoids : public Integral {
private:
  // Metodo dei trapezi con NUMERO DI PASSI fissato (come negli esercizi 7.0 e 7.1)
  double calculate(int nstep, const FunzioneBase & f) override { ... }

public:
  // Metodo dei trapezi con PRECISIONE FISSATA (nuovo!). Questo metodo si
  // implementa direttamente come pubblico
  double integrate_prec(double a, double b, double prec, const FunzioneBase & f) {
    ...
  }
};
```

Un algoritmo a precisione fissata si può implementare anche per il metodo midpoint e per il metodo di Simpson ma nel caso dei trapezoidi si presta ad una implementazione particolarmente efficiente (si veda la sezione sotto).

Il metodo dei trapezi

Il metodo dei trapezi rappresenta la prima formula chiusa di Newton-Cotes e si basa su una interpolazione polinomiale di ordine 1 sui due punti che delimitano l’intervallo. La formula che approssima l’integrale è

\int_a^b f(x)\,\mathrm{d}x \approx \left(\frac12 f(x_0) + f(x_1) + \dots + f(x_{N - 1}) + \frac12 f(x_N)\right)h,

dove

h = \frac{b - a}N

x_k = a + k h, \qquad k = 0, 1, \ldots N.

Stima runtime dell’errore

Come possiamo stimare l’errore che stiamo commettendo nel calcolo di un integrale se non conosciamo il valore vero I dell’integrale? Partendo dalla conoscenza dell’andamento teorico dell’errore in funzione del passo h, possiamo trovare un modo semplice per la stima dell’errore che stiamo commettendo. Nel caso della regola dei trapezi, l’adamento dell’errore è \epsilon = k h^2. Calcolando l’integrale I_N utilizzando un passo h e successivamente l’intgrale I_{2N} con un passo h/2, possiamo scrivere il seguente sistema di equazioni: \begin{cases} I - I_N = k h^2,\\ I - I_{2N} = k\left(\frac{h}2\right)^2. \end{cases}

Sottraendo per esempio la prima equazione alla seconda, non è difficile ricavare che una stima dell’errore pari a \epsilon(N) = \frac43 \left|I_{2N} - I_N\right|.

Cenni sull’implementazione

La condizione di uscita dell’algoritmo è basata sul confronto del risultato di due passaggi successivi. Se la differenza della stima dell’integrale tra due passaggi consecutivi è più piccola della precisione richiesta allora l’algoritmo si ferma. Questo poiché l’integrale calcolato con una partizione più fine è sempre una stima migliore dell’approssimazione con la partizione originaria. L’algoritmo dei trapezoidi si presta ad una implementazione ottimizzata descritta qui di seguito. Nel costruttore calcoliamo la prima approssimazione:

\begin{cases} \Sigma_0 &= \frac{f(a) + f(b)}2,\\ I_0 &= \Sigma_0 \times (b - a). \end{cases}

Al primo passo dell’algoritmo suddividiamo l’intervallo in due:

\begin{cases} \Sigma_1 = \Sigma_0 + f\left(x_{11}\right),\\ I_1 = \Sigma_1 \times \frac{b - a}2. \end{cases}

Al secondo passaggio otteniamo

\begin{cases} \Sigma_2 = \Sigma_1 + f\left(x_{21}\right) + f\left(x_{22}\right),\\ I_2 = \Sigma_2 \times \frac{b - a}4. \end{cases}

Al terzo passaggio otteniamo

\begin{cases} \Sigma_3 = \Sigma_1 + f\left(x_{31}\right) + f\left(x_{32}\right) + f\left(x_{33}\right) + f\left(x_{34}\right),\\ I_3 = \Sigma_3 \times \frac{b - a}8. \end{cases} e così via secondolo schema in figura, con L = b - a:

I valori dell’ultima approssimazione dell’integrale e dell’ultima somma calcolata sono memorizzati all’interno dell’oggetto. In questo modo, se viene richiesto di ricalcolare l’integrale, non è necessario ricominciare da capo.

Test

Esercizio 7.3 - Integrazione di una funzione Gaussiana (facoltativo)

Come esercizio facoltativo vi proponiamo il calcolo di un integrale non risolubile analiticamente. Assumendo che una misura abbia un valore vero \mu e una deviazione standard \sigma, calcoliamo la probabilità che una misura cada entro \pm t\sigma dal valore vero per t che va da 0 a 5. La probabilità è ovviamente data dalla distribuzione Gaussiana:

f(x) = \frac1{\sqrt{2\pi\sigma^2}} \exp\left(-\frac{(x - \mu)^2}{2\sigma^2}\right).

Costruite una classe Gaussian generica. I parametri \mu e \sigma della funzione f(x) possono essere passati nel costruttore.
Integrate la funzione Gaussiana con il metodo dei trapezi a precisione fissata in un intervallo [\mu - t\sigma, \mu + t\sigma] con t variabile da 0 a 5.
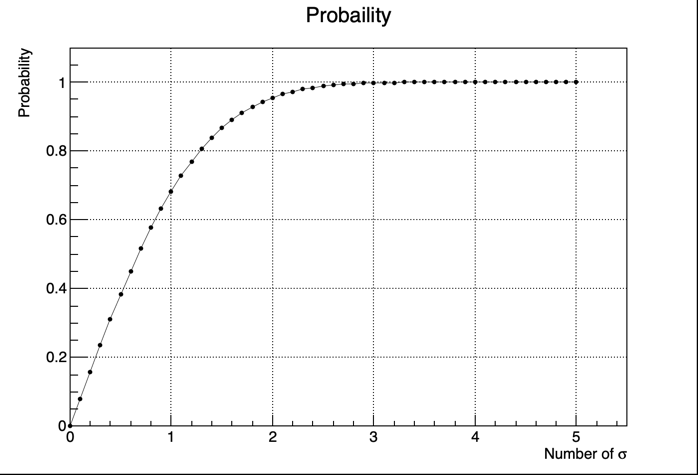
Producete un grafico dell’integrale ottenuto in funzione del numero di \sigma. Vi torna?

Il risultato non dovrebbe sorprendere:

Errori comuni

Come di consueto, elenco alcuni errori molto comuni che ho trovato negli anni passati correggendo gli esercizi che gli studenti hanno consegnato all’esame:

Molte volte gli studenti usano la funzione abs anziché fabs nel determinare l’ampiezza dell’intervallo di integrazione. Attenzione! Se fabs restituisce sempre un numero floating-point, la funzione abs lo fa solo se si include <cmath>, altrimenti restituisce un intero: se quindi non includete <cmath> e l’intervallo di integrazione b-a è inferiore a 1, avrete che abs(b - a) == 0!
Alcuni studenti calcolano le somme dei termini degli integrali saltando l’ultimo punto a destra dell’intervallo (e sottostimando quindi l’integrale di h \cdot \pi/2 \cdot \sin \pi/2).
Attenzione ai coefficienti nella formula di Simpson, perché a volte gli studenti scambiano di posto il 4 con il 2!
Non confondete il significato di “numero di passi” quando calcolate l’errore di un metodo di integrazione: se per calcolare l’errore dovete stimare l’integrale con passo h e con passo h/2, l’errore che ottenete si riferisce al passo h, non al passo h/2! (Va detto però che quest’errore è più frequente negli esami scritti che negli esercizi.)

Il notebook all’indirizzo https://ziotom78.github.io/tnds-notebooks/lezione07/ fornisce una lunga serie di test: se li implementate tutti, avete il 99.9% di essere sicuri che la vostra implementazione sia corretta!