[La pagina con la spiegazione originale degli esercizi si trova qui: https://labtnds.docs.cern.ch/Lezione5/Lezione5/.]

In questa quinta lezione vogliamo affrontare un semplice problema di elettrostatica utilizzando un codice numerico. In particolare, vogliamo calcolare il campo elettrico generato da un dipolo. Vedremo poi come il codice si può estendere in modo immediato a problemi più complessi (ad esempio per studiare il campo generato da un multi-polo o il campo gravitazionale generato da un sistema di masse). Nell’affrontare questo problema fisico approfondiremo il concetto di ereditarietà in C++. Come al solito dovremo prima preparare un set di classi utili per lo svolgimento dell’esercizio.

Esercizio 5.0 - Creazione della classe Posizione

Implementare una classe Posizione che descriva un punto nello spazio seguendo queste indicazioni:

1. Come data membri privati usare la terna di coordinate cartesiane.
2. Definire un costruttore di default che crei un punto di coordinate (0,0,0).
3. Definire un costruttore che abbia come argomento una terna di numeri double corrispondenti alle coordinate del punto.
4. Definire metodi per restituire le coordinate del punto in sistemi di coordinate cartesiane, sferiche e cilindriche.
5. Definire un metodo che calcoli la distanza da un altro punto.

Verificare il funzionamento della classe creando un programmino che legga da riga di comando le coordinate cartesiane di un punto e ne stampi le coordinate in un sistema di coordinate sferiche e cilindriche.

Header file della classe

Nell’header file posizione.h vanno dichiarati tutti i metodi ed i data membri. Si noti come i data membri siano tutti privati: questa modo di disegnare le classi implementa il concetto di incapsulamento e data hiding in C++.

Un paio di punti già che vale la pena ricordare:

1. Il qualificatore const dopo la dichiarazione di una funzione informa che la funzione non modificherà il contenuto dell’oggetto. In maniera simile il qualificatore const nell’argomento di Distanza specifica che il metodo Distanza non modificherà il suo argomento. È sempre utile specificare esplicitamente queste proprietà dei metodi.
2. L’insieme dell direttive #ifndef, #define, #endif serve per proteggersi da inclusioni incrociate (molto comuni quando si utilizzano diverse classi che interagiscono tra di loro). Nelle slide abbiamo però visto che #pragma once è un modo più semplice di ottenere lo stesso risultato che mette al riparo da tanti potenziali errori.

#pragma once

class Posizione {
public:
  // costruttori
  Posizione();
  Posizione(double x, double y, double z);

  // distruttore
  ~Posizione();

  // metodi
  double getX() const; // Coordinate cartesiane
  double getY() const;
  double getZ() const;
  double getR() const; // Coordinate sferiche
  double getPhi() const;
  double getTheta() const;
  double getRho() const; // raggio delle coordinate cilindriche
  double Distanza(const Posizione &) const; // distanza da un altro punto

private:
  double m_x, m_y, m_z;
};

File di implementazione delle classe

Qui vediamo un esempio di implementazione della classe (file posizione.cpp). Per prima cosa sono definiti i costruttori ed un distruttore, che in questo caso può esser vuoto (nei costruttori non ci sono operazioni di allocazione dinamica della memoria quindi non è necessario implementare regole di distruzione particolari). Noi definiamo comunque il distruttore, perché questo è un esempio didattico; solitamente per classi così semplici però il distruttore si tralascia se il suo corpo è vuoto ({}). Successivamente sono implementati tutti i metodi descritti nell’header file:

#include "posizione.h"
#include <cmath>

// costruttore di default
Posizione::Posizione() : m_x{}, m_y{}, m_z{} {}

// costruttore a partire da una terna cartesiana
Posizione::Posizione(double x, double y, double z) : m_x{x}, m_y{y}, m_z{z} {}

// distruttore (puo' essere vuoto)
Posizione::~Posizione() {}

// Coordinate cartesiane

double Posizione::getX() const { return m_x; }
double Posizione::getY() const { return m_y; }
double Posizione::getZ() const { return m_z; }

// Coordinate sferiche

double Posizione::getR() const {
  return sqrt(m_x * m_x + m_y * m_y + m_z * m_z);
}

double Posizione::getPhi() const { return atan2(m_y, m_x); }

double Posizione::getTheta() const { return acos(m_z / getR()); }

// raggio delle coordinate cilindriche

double Posizione::getRho() const { return sqrt(m_x * m_x + m_y * m_y); }

// distanza da un altro punto
double Posizione::Distanza(const Posizione &b) const {
  return sqrt(pow(getX() - b.getX(), 2) +
              pow(getY() - b.getY(), 2) +
              pow(getZ() - b.getZ(), 2));
}

Esempio di programma

Questo programma utilizza la nuova classe appena creata: richiede di fornire come argomenti le tre coordinate cartesiane e poi stampa le terne di coordinate cartesiane, sferiche e cilindriche.

Il programma è pensato per usare la libreria fmt, che potete installare usando lo script install_fmt_library: scaricatelo nella directory dell’esercizio ed eseguitelo con sh install_fmt_library, oppure eseguite questo comando:

Copia

(Se invece usate Windows, scaricate questo file zip nella directory dell’esercizio e decomprimetelo). Le istruzioni dettagliate sono in questa pagina.

#include "posizione.h"

// Installarla con ./install_fmt_library
#include "fmtlib.h"

#include <iostream>
#include <string>

using namespace std;

// Questo programma richiede da riga di comando le coordinate x, y e z di
// un punto e ne restituisce le coordinate sferiche e cilindiriche.

int main(int argc, char *argv[]) {
  // Controlla gli argomenti
  if (argc != 4) {
    fmt::println(stderr, "Usage: {} X Y Z", argv[0]);
    return -1;
  }

  double x{stod(argv[1])};
  double y{stod(argv[2])};
  double z{stod(argv[3])};

  // Crea un oggetto posizione ed accede ai vari metodi

  Posizione P{x, y, z};

  // Invece di `cout`, usiamo fmtlib: molto più comodo!
  fmt::println("Coordinate cartesiane: {}, {}, {}",
               P.getX(), P.getY(), P.getZ());
  fmt::println("Coordinate cilindriche: {}, {}, {}",
               P.getRho(), P.getPhi(), P.getZ());
  fmt::println("Coordinate sferiche: {}, {}, {}",
               P.getR(), P.getPhi(), P.getTheta());

  return 0;
}

Questo è un esempio di output del programma:

$ ./test 1 2 5
Coordinate cartesiane: 1, 2, 5
Coordinate cilindriche: 2.23606797749979, 1.1071487177940904, 5
Coordinate sferiche: 5.477225575051661, 1.1071487177940904, 0.420534335283965

Incapsulamento e data hiding

Utilizziamo l’esempio della classe Posizione per riflettere sul concetto di incapsulamento. La nostra classe “nasconde” i dati principali (le tre coordinate nel caso specifico) in un set di data-membri privati (m_x, m_y, m_z). Tali data-membri non sono per definizione accessibili al programma principale in modo diretto, ma solo attraverso una serie di metodi pubblici (interfacce) che proteggono il dato da un utilizzo incontrollato. Inoltre la protezione del dato dietro interfacce pubbliche mette al riparo da possibili cambiamenti o correzioni nel design di una classe.

Per fare un esempio, supponiamo che per qualche ragione l’autore della classe decida che è meglio rappresentare la posizione utilizzando una terna di numeri che corrispondono alle coordinate sferiche. Se l’autore della classe adegua di conseguenza le interfacce pubbliche, un eventuale utilizzatore della classe (il nostro main) non si accorgerebbe della variazione. Se invece il main`` avesse avuto libero accesso alle tre coordinate e le avesse utilizzate direttamente, il cambiamento di design della classe avrebbe richiesto rendendo pesanti cambiamenti anche nelmain``.

Una nota sui distruttori

L’implementazione esplicita di un distruttore è spesso necessaria per evitare memory leaks quando il costruttore alloca dinamicamente memoria. In caso contrario tipicamente il distruttore sarà vuoto e può essere omesso. Ricordiamoci che se il distruttore viene dichiarato nell’header file della classe allora dobbiamo necessariamente fornirne una implementazione (anche vuota). In questo caso in posizione.h ci basta scrivere:

~Posizione() {}

Esercizio 5.1 - Creazione della classe Particella ed Elettrone

Incominciamo a definire due classi che ci permetteranno di rappresentare le sorgenti del campo (elettrico in questo caso).

• Costruiamo una classe Particella caratterizzata dall’avere una massa ed una carica, quindi dotata dei seguenti metodi:

  1. Un construttore avente come argomenti massa e carica.

  2. Dei metodi di accesso ai valori di massa e carica.

  3. Un metodo per stampare tali valori.

• Siccome vogliamo che questa classe sia la classe base di altre classi, dichiareremo i data membri come protected.

• Costruiamo, attraverso il meccanismo di ereditarietà, una classe derivata Elettrone che, essendo una Particella di massa e carica note (i cui valori sono riportati su wikipedia), ha il solo costruttore di default, che inizializza correttamente i data membri. Modifichiamo il metodo di stampa in modo che indichi che si tratta di un elettrone.

Verifichiamo che le nuovi classi e l’ereditarietà funzioni correttamente:

1. Istanziamo dinamicamente un oggetto per ogni classe.
2. Verifichiamo che su tutti questi operino i metodi accessori di massa e carica di Particella, ma il metodo di stampa delle classi derivate.

Classe Particella

Questo è l’header particella.h per la classe Particella:

#pragma once

// Classe astratta per una generica particella
// Definisce i metodi che ogni particella
// deve implementare e delle funzioni di utilizzo generale.

class Particella {
public:
  // costruttori
  Particella();
  Particella(double massa, double carica);

  // distruttore (vuoto, si può anche omettere)
  ~Particella() {}

  // metodi

  double GetMassa() const { return m_massa; }
  double GetCarica() const { return m_carica; }
  void Print() const;

protected:
  double m_massa;
  double m_carica;
};

Implementazione nel file particella.cpp:

#include "fmtlib.h"

// Metodi per la classe base

Particella::Particella(double massa, double carica)
  : m_massa{massa}, m_carica{carica} {}

void Particella::Print() const {
  fmt::println("Particella: m = {}, q = {}", m_massa, m_carica);
}

Classe Elettrone

File header elettrone.h per la classe Elettrone (in questo caso scegliamo di tenere tutto nel file .h, e non c’è bisogno quindi di creare un file elettrone.cpp: molto più comodo!):

#pragma once

#include "fmtlib.h"

// Implementazione concreta di una particella elementare
// In questo caso tutte le proprietà della particella
// sono costanti, definite nel costruttore di default.

class Elettrone : public Particella {
public:
  // Costruttore
  Elettrone() : Particella{9.1093826e-31, -1.60217653e-19} {
      // Invoco il costruttore della classe base con i parametri
      // opportuni,  ma poi non c'e' altro da fare
  }

  // Distruttore (vuoto, si può omettere)
  ~Elettrone() {}

  void Print() const {
      fmt::println("Elettrone: m = {}, q = {}", m_massa, m_carica);
  }
};

Esempio di programma

Questo programma utilizza le nuove classi appena create. Verifica il funzionamento dell’ereditarietà e la dereferenziazione dei puntatori a classe.

#include "fmtlib.h"
#include "particella.h"
#include <iostream>

using namespace std;

int main() {
  // `a` è una variabile di tipo `Particella`
  Particella a{1., 1.6E-19};
  // `e` è un *puntatore* a una variabile di tipo `Elettrone`
  Elettrone *e{new Elettrone{}};

  // Metodi della classe base. Notare che qui la sintassi è `a.NOMEMETODO(…)`
  fmt::println("Particella con massa {} kg e carica {} C", a.GetMassa(),
               a.GetCarica());
  a.Print();

  // Metodi della classe derivata. Qui invece la sintassi è
  // `e->NOMEMETODO(…)` e non `e.NOMEMETODO(…)`,
  // perché `e` è un puntatore
  fmt::println("Elettrone con massa {} kg e carica {} C", e->GetMassa(),
               e->GetCarica());
  e->Print();

  Particella b{a};  // costruisco una Particella a partire da una Particella
  Particella d{*e}; // costruisco una Particella a partire da un Elettrone
  Elettrone f{d};   // costruisco un Elettrone a partire da una Particella

  return 0;
}

Domanda

Il programma di esempio contiene un errore, lo trovate?

Esercizio 5.2 - Creazione delle classi CampoVettoriale e PuntoMateriale

Per risolvere problemi relativi all’elettrostatica o alla gravità proviamo ad effettuare una modellizzazione basata su due elementi principali: una rappresentazione del campo vettoriale e una rappresentazione delle sorgenti dei campi vettoriali.

Definiremo quindi una classe CampoVettoriale: sono molti i casi in Fisica in cui un vettore è collegato ad un punto dello spazio. Ad esempio una forza ha un punto di applicazione, o i vettori del campo elettrico e campo gravitazionale hanno un valore che varia da punto a punto dello spazio.

Questo esercizio richiede di costruire una classe CampoVettoriale, che erediti dalla classe Posizione e che aggiunga:

1. le tre componenti di un vettore alla posizione;

2. i metodi per accedere e/o modificare il vettore;

3. costruttori: in particolare, il costruttore CampoVettoriale(const Posizione&) che crei un vettore nullo nella posizione assegnata;

4. un metodo double Modulo() const che restituisca la lunghezza del vettore;

5. overloading di operator+ e operator+= in modo da poter facilmente sommare campi.

Header file della classe CampoVettoriale

#pragma once

#include "posizione.h"

class CampoVettoriale : public Posizione {
public:
  CampoVettoriale(const Posizione &);
  CampoVettoriale(const Posizione &,
                  double Fx, double Fy, double Fz);
  CampoVettoriale(double x, double y, double z,
                  double Fx, double Fy, double Fz);

  // Distruttore (vuoto, si può tralasciare)
  ~CampoVettoriale() {}

  // Operatore di incremento
  void operator+=(const CampoVettoriale &);

  double getFx() const { return m_Fx; }
  double getFy() const { return m_Fy; }
  double getFz() const { return m_Fz; }
  double Modulo() const;

private:
  double m_Fx, m_Fy, m_Fz;
};

// Somma di due campi vettoriale (in una funzione,
// non in un metodo!)
inline CampoVettoriale operator+(const CampoVettoriale &a,
                                 const CampoVettoriale &b) {
  // …
}

Abbiamo scelto di implementare la somma di due campi vettoriali come una funzione anziché un metodo, quindi non è definita all’interno delle parentesi graffe di class CampoVettoriale : public Posizione { … }. Sarebbe stato possibile definire un metodo in base al fatto che per il compilatore C++ la scrittura

c = a + b;

è equivalente a

c = a.operator+(b);

Avremmo quindi potuto definire un metodo

CampoVettoriale CampoVettoriale::operator+(const CampoVettoriale &b) {
  // …
}

Questa pratica è però scoraggiata negli operatori binari come la somma, perché è poco leggibile: infatti a differenza della forma funzionale, a non è esplicito in questo caso (equivale a *this).

Overloading operatori

Per risolvere facilmente questo tipo di problemi è molto utile ridefinire gli operatori operator+ e operator+= per la classe CampoVettoriale. Di seguito una possibile implementazione comoda di questo overloading. Notate che nell’operatore operator+ viene creato un nuovo vettore (sum) che viene restituito by value. Per operator+= invece la modifica viene effettuata sull’oggetto che chiama l’operatore. L’oggetto stesso (modificato) viene poi restituito by reference.

inline CampoVettoriale operator+(const CampoVettoriale &a,
                                 const CampoVettoriale &b) {
  if ((a.getX() != b.getX()) ||
      (a.getY() != b.getY()) ||
      (a.getZ() != b.getZ())) {
      // fmt::print accetta come primo argomento lo stream su cui
      // scrivere (se non si specifica, usa stdout, che è analogo a std::cout).
      // Siccome questo è un messaggio di errore, usiamo stderr, analogo a
      // std::cerr
      fmt::println(stderr,
                   "Somma di campi vettoriali in punti diversi non ammessa");
      exit(1);
  }

  CampoVettoriale sum{
      a.getX(),
      a.getY(),
      a.getZ(),
      a.getFx() + b.getFx(),
      a.getFy() + b.getFy(),
      a.getFz() + b.getFz(),
  };

  return sum;
}

// Ricordare che, se `v` e `w` sono due oggetti di tipo `CampoVettoriale`, allora
//
//    w += v;
//
// viene considerato dal compilatore C++ come
//
//    w.operator+=(v);
void CampoVettoriale::operator+=(const CampoVettoriale & v) {
  // Non c'è bisogno di usare le funzioni getFx(), getFy(), getFz():
  // siamo in un metodo di CampoVettoriale, quindi abbiamo accesso
  // ai membri privati (non è così per operator+ definito sopra)

  m_Fx += v.m_Fx;
  m_Fy += v.m_Fy;
  m_Fz += v.m_Fz;
}

In alcuni codici si può trovare l’operatore di incremento che restituisce un reference all’istanza stessa della classe che ha subito l’incremento (*this):

CampoVettoriale & CampoVettoriale::operator+=(const CampoVettoriale & v) {
  // …

  return *this;
}

Il fatto di tornare un CampoVettoriale & anziché un void permette di usare la scrittura

c = a += b;

che per il compilatore C++ è equivalente a

c = a.operator+=(b);

e corrisponde ai seguenti passaggi:

1. Incremento di a del campo b;

2. Una volta che a è stato incrementato, assegnamento del valore risultante a c.

Noi non useremo mai la scrittura c = a += b, perché è difficile da leggere e mai realmente utile; è infatti più chiaro spezzare la riga in due istruzioni:

a += b;
c = a;

N.B.: per entrambe le classi di cui sopra, sentitevi liberi di aggiungere tutti i metodi addizionali che ritenete utili per risolvere questo esercizio o i successivi.

Header file della classe PuntoMateriale

La classe PuntoMateriale ci servirà per rappresentare le sorgenti dei campi.

Ereditarietà multipla

In C++, una classe può ereditare da più di una classe madre. In questo caso mantiene le proprietà (metodi e data membri) di tutte le classi madri. Nell’header file puntomateriale.h vanno elencate tutte le classi da cui si vuole ereditare, specificando la modalità con cui si vuole ereditare (public, private o protected):

#pragma once

#include "particella.h"
#include "posizione.h"

class PuntoMateriale : public Particella, public Posizione {
    // …
};

La nuova classe avrà, per esempio, definiti sia i metodi GetMassa() e GetCarica() di Particella e anche GetX(), GetR(), … di Posizione.

Utilizzo di costruttori delle classi madri

Specialmente nel caso di ereditarietà multipla, è buona norma utilizzare i costruttori già esistenti della classe madre. Tali costruttori possono venire chiamati esplicemente dando il nome della classe madre seguito dagli argomenti opportuni. Ad esempio, siccome esistono i costruttori di Posizione con le tre coordinate cartesiane, e di Particella con massa e carica, possiamo definire un costruttore:

PuntoMateriale(double massa, double carica, double x, double y, double z);

la cui implementazione è data da:

PuntoMateriale::PuntoMateriale(double massa, double carica,
                               double x, double y, double z) :
    Particella{massa, carica}, Posizione{x, y, z} {

    // nothing more to be done !
}

Come si può notare in questo esempio la costruzione di PuntoMateriale è completamente delegata si costruttori delle classi madre.

Esercizio 5.3 - Calcolo del campo elettrico generato da un dipolo (da consegnare)

A questo punto possiamo utilizzare tutti gli ingredienti realizzati sopra per affrontare un interessante problema di elettrostatica ovvero lo studio del campo elettrico generato da un dipolo. Per fare questo sviluppiamo un codice che costuisca un dipolo costituito da un elettrone e un protone posizionati ad una distanza \delta = 10^{-10}\,\text{m} e determini:

1. il valore del campo elettrico di dipolo prodotto in un punto P le cui coordinate sono inserite da linea di comando;
2. disegni l’andamento del modulo del campo elettrico lungo l’asse del dipolo per una distanza da 100 a 1000 volte \delta. Che tipo di andamento ha il campo? (Fate riferimento all’approfondimento seguente sulle leggi di potenza qui sotto).

Esempio di programma

Questo programma utilizza le nuove classi appena create: richiede di fornire come argomenti le tre coordinate cartesiane e poi stampa il campo elettrico di dipolo richiesto dall’esercizio [primo punto]:

#include "puntomateriale.h"
#include "campovettoriale.h"

#include "fmtlib.h"

#include <iostream>
#include <string>

using namespace std;

const double e{1.60217653E-19};
const double me{9.1093826E-31};
const double mp{1.67262171E-27};
const double d{1.E-10};

int main(int argc, char * argv[]) {
  if (argc != 4) {
      fmt::println(stderr, "Usage: {} <x> <y> <z>", argv[0]);
      exit(1);
  }

  double x{stod(argv[1])};
  double y{stod(argv[2])};
  double z{stod(argv[3])};
  Posizione r{x,y,z};

  PuntoMateriale elettrone{me, -e, 0, 0,  d / 2};
  PuntoMateriale protone  {mp,  e, 0, 0, -d / 2};

  CampoVettoriale E{elettrone.CampoElettrico(r) + protone.CampoElettrico(r)};
  fmt::println("E = ({}, {}, {}) N/C", E.getFx(), E.getFy(), E.getFz());

  return 0;
}

A partire da questo esempio completare le richieste dell’esercizio:

• Si aggiunga un ciclo che permetta di calcolare il campo a distanze via via crescenti

• Si aggiunga eventualmente un grafico per visualizzare l’andamento del campo in funzione della distanza dal centro del dipolo. Potete usare ROOT o gplot++.

Il Makefile

Il numero di classi sta proliferando e quindi anche il Makefile diventa sempre più articolato. Questo esempio è pensato per ROOT:

INCS=`root-config --cflags`
LIBS=`root-config --libs`
CXXFLAGS=-g -Wall --pedantic -std=c++23

esercizio_5.3: esercizio_5.3.o posizione.o puntomateriale.o campovettoriale.o particella.o
       g++ -o esercizio_5.3 esercizio_5.3.o posizione.o puntomateriale.o campovettoriale.o particella.o ${LIBS}

esercizio_5.3.o: esercizio_5.3.cpp particella.h puntomateriale.h posizione.h campovettoriale.h
       g++ -c esercizio_5.3.cpp -o esercizio_5.3.o ${INCS} ${CXXFLAGS}

particella.o: particella.cpp particella.h
       g++ -c particella.cpp -o particella.o ${CXXFLAGS}

posizione.o: posizione.cpp posizione.h
       g++ -c posizione.cpp -o posizione.o ${CXXFLAGS}

puntomateriale.o: puntomateriale.cpp puntomateriale.h posizione.h particella.h
       g++ -c puntomateriale.cpp -o puntomateriale.o ${CXXFLAGS}

campovettoriale.o: campovettoriale.cpp campovettoriale.h posizione.h
       g++ -c campovettoriale.cpp -o campovettoriale.o ${CXXFLAGS}

clean:
       rm -f *.o

Questo invece è il caso in cui usiate gplot++: non c’è più bisogno di usare INCS e LIBS.

CXXFLAGS=-g -Wall --pedantic -std=c++23

esercizio_5.3: esercizio_5.3.o posizione.o puntomateriale.o campovettoriale.o particella.o
       g++ -o esercizio_5.3 esercizio_5.3.o posizione.o puntomateriale.o campovettoriale.o particella.o

esercizio_5.3.o: esercizio_5.3.cpp particella.h puntomateriale.h posizione.h campovettoriale.h
       g++ -c esercizio_5.3.cpp -o esercizio_5.3.o ${CXXFLAGS}

particella.o: particella.cpp particella.h
       g++ -c particella.cpp -o particella.o ${CXXFLAGS}

posizione.o: posizione.cpp posizione.h
       g++ -c posizione.cpp -o posizione.o ${CXXFLAGS}

puntomateriale.o: puntomateriale.cpp puntomateriale.h posizione.h particella.h
       g++ -c puntomateriale.cpp -o puntomateriale.o ${CXXFLAGS}

campovettoriale.o: campovettoriale.cpp campovettoriale.h posizione.h
       g++ -c campovettoriale.cpp -o campovettoriale.o ${CXXFLAGS}

clean:
       rm -f *.o

Nel caso in cui decidiate di implementare tutte le classi nei file .h e di non usare quindi file .cpp, il Makefile si semplifica moltissimo. Ecco un esempio (assumendo che usiate gplot++):

CXXFLAGS=-g -Wall --pedantic -std=c++23

esercizio_5.3: esercizio_5.3.cpp posizione.h puntomateriale.h campovettoriale.h particella.h
       g++ -o esercizio_5.3 esercizio_5.3.cpp ${CXXFLAGS}

clean:
       rm -f *.o

Leggi di potenza

Se un campo ha un andamento E = k R^\alpha e valutiamo il campo in due punti diversi R_1 e R_2: E_1 = E(R_1), \qquad E_2 = E(R_2), allora possiamo ricavare \alpha dalla relazione \alpha = \frac{\log\bigl(E_1 / E_2\bigr)}{\log\bigl(R_1 / R_2\bigr)}

Creazione di plot

Potete fare riferimento a questa spiegazione per produrre un grafico dell’andamento del campo usando la classe TGraph di ROOT.

In alternativa potete usare gplot++, che funziona sotto Mac e Linux ed è semplice da installare anche sotto Windows. Dovete innanzitutto installare Gnuplot, seguendo in particolare questa avvertenza se usate Windows. Una volta installato Gnuplot, scaricate nella directory del vostro esercizio il file gplot++.h, oppure se usate Linux o Mac eseguite questa linea di comando nella directory del vostro esercizio:

Copia

Per produrre un grafico di E = E(r) con gplot++, dovete salvare le ascisse e le ordinate dei punti del grafico in due std::vector, e poi chiamare il metodo Gnuplot::plot(x, y).

Di seguito viene riportato un esempio:

#include "fmtlib.h"
#include "gplot++.h"

// ...

using namespace std;

const double delta = 1e-10;

// Siccome questo programma non richiede di leggere parametri dalla linea di
// comando, non c'è bisogno di specificare "argc" e "argv". (Se lo faceste,
// il compilatore probabilmente emetterebbe qualche tipo di warning, perché
// l'argomento è stato dichiarato ma mai usato).
int main() {
  vector<double> d_vec; // Vettore delle distanze (asse x)
  vector<double> E_vec; // Vettore dei moduli del campo elettrico (asse y)

  // Questo ciclo "for" calcola il valore del campo per 90 punti,
  // da 100δ a 1000δ in passi di 10δ
  for (double dist{100 * delta}; dist <= 1000 * delta; dist += 10 * delta) {
    // Il vettore `d_vec` è usato per la stampa a video e il plot, non per i
    // calcoli, quindi è meglio salvare il dato in nm anziché m (è più leggibile).
    d_vec.push_back(dist * 1e9);

    // Inserire qui il codice che calcola il modulo del campo alla distanza
    // `dist`
    double e_field{...};

    E_vec.push_back(e_field);

    // Stampa anche a video: è sempre bene farlo per controllare i numeri!
    fmt::println("{:.5e} {:.5e}", dist, e_field);
  }

  Gnuplot plt{};

  // Togliere questa riga se si preferisce che il grafico appaia in una finestra
  // interattiva (consigliato sul proprio computer o su quelli del laboratorio,
  // sconsigliato se si usa Repl.it)
  plt.redirect_to_png("esercizio05.3.png");

  // Disegna le ascisse usando una scala bilogaritmica, così che y ∝ 1/r³ viene
  // trasformato in una legge lineare y' = ξ − 3r', con y' = log(y), r' = log(r).
  plt.set_logscale(Gnuplot::AxisScale::LOGXY);
  plt.set_xlabel("Distance [nm]");
  plt.set_ylabel("Electric field [N/C]");

  plt.plot(d_vec, E_vec);

  // Ricordarsi di chiamarlo, altrimenti il grafico non verrà salvato/visualizzato
  plt.show();
}

Questo è il risultato atteso:

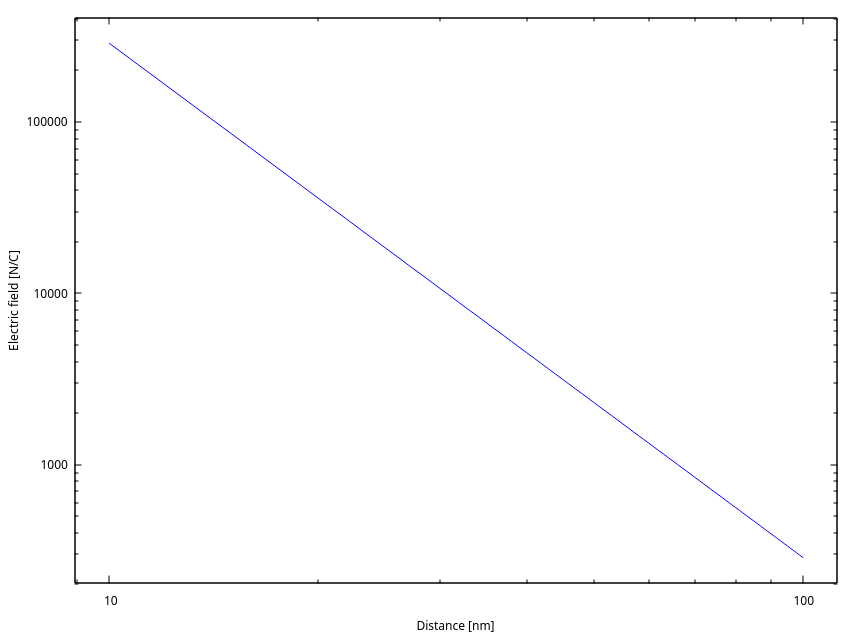
Notare che la pendenza della retta sul grafico bilogaritmico è −3: per un ordine di grandezza in più sull’asse x (da 10 a 100 nm) ci sono tre ordini di grandezza in meno (da 5 \times 10^5 a 500\,\text{N/C}) sull’asse y. Questo corrisponde al fatto che se r \gg \delta allora \left|E_\text{dipolo}(r)\right| = \left|k\frac{q^+}{(r + \delta)^2} + k\frac{q^-}{(r - \delta)^2}\right| = \left|k\frac{e}{(r + \delta)^2} - k\frac{e}{(r - \delta)^2}\right| \approx \frac{4 k e \delta}{r^3} \propto r^{-3}.

Esercizio 5.4 - Campo di multipolo (approfondimento)

Scrivere un programma che calcoli il campo elettrico generato da un multipolo di ordine n. In questo esercizio, un n-polo (con n pari) è una distribuzione di n particelle, in cui la particella k-esima ha carica (-1)^k e, dove e è la carica del protone, e si trova nel punto P_k = \left(r_0 \cos\left(\frac{2\pi k}n\right), r_0 \sin\left(\frac{2\pi k}n\right)\right) dove r_0 è il raggio a cui sono messe le cariche.

• Verificare che a grande distanza (R \gg r_0) il campo elettrico varia proporzionalmente a R^{-2 - n/2}.

• Valutare fino a quali valori di n si riesce a verificare questa dipendenza.

Questo è un problema abbastanza interessante, perché bisogna scegliere una distanza abbastanza grande perché sia valido il comportamento asintotico, ma abbastanza ridotta per evitare problemi di arrotondamento nella somma di molti termini di segno contrario.

Esercizio 5.5 - Gravità dallo spazio (approfondimento)

Il satellite GOCE si trova in orbita a 250 km dalla superficie terrestre e dotato di accelerometri in grado di misurare variazioni dell’accelerazione di gravità fino a \delta g / g = 10^{-13}. Lo scopo della missione includeva una mappatura dettagliata del campo gravitazionale terrestre, prodotto dalle distribuzioni non omogenee di massa. Costruire un programma che:

1. calcoli l’accelerazione di gravità sul satellite per una Terra perfettamene sferica e dimensioni pari al raggio medio (wikipedia).
2. calcoli la variazione relativa di g prodotta da una catena montuosa, schematizzata come una fila di 100 sfere di 1 km di raggio poste sopra la superficie media della Terra (usare 3000 kg/m³ come densità della roccia) e produca un grafico della variazione in funzione della posizione del satellite sull’orbita.

Per risolvere questo esercizio si costruisca dapprima il sistema di sorgenti di campo (Terra e catena montuosa). Si calcoli il campo generato da tutte le sorgenti in un punto a distanza dal centro della terra pari al raggio terrestre più la distanza del satellite dalla superficie terrestre. Muovere questo punto in modo che percorra tutta l’orbita (in passi da 10 Km).

Grafici

Nel creare un grafico dell’andamento della distorsione dell’accelerazione gravitazionale \delta g / g è meglio usare la scala logaritmica sull’asse y, visto che il valore di \delta g/g varia di diversi ordini di grandezza:

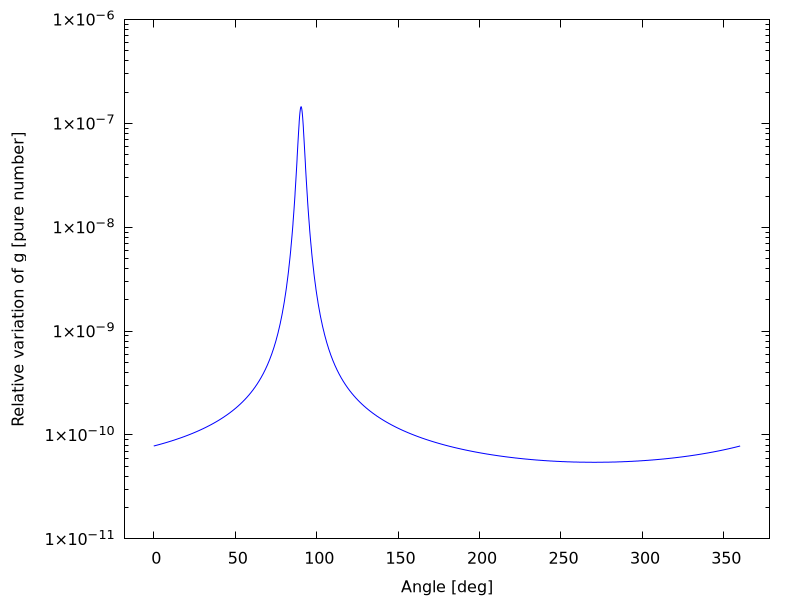
La posizione del picco dipende dal punto rispetto all’angolo zero in cui sono state poste le sfere che rappresentano la catena montuosa. Nel grafico qui sopra, la montagna k-esima è stata posta ad un angolo \theta_k = 90^\circ + k \delta\theta, con k = 0\ldots 99 e \delta\theta = 1\,\text{km} / 2\pi R_T l’incremento angolare associato a sfere di raggio 1 km e poste sulla superficie terrestre, con R_T raggio medio della Terra.

Errori comuni

Come di consueto, elenco alcuni errori molto comuni che ho trovato negli anni passati correggendo gli esercizi che gli studenti hanno consegnato all’esame:

• L’errore di gran lunga più comune è sbagliare l’implementazione della formula del campo, che oggettivamente è complicata! Riguardate in particolare queste cose:

  1. Unità di misura delle costanti;

  2. Attenzione a come scrivete i numeri in notazione scientifica! Il numero 10^{-4} si scrive 1e-4, non 10e-4, perché la scrittura 1e-4 indica effettivamente 1 \times 10^{-4}, così come 7.5e-3 indica 7.5\times 10^{-3}.

  3. Verificate che ciò che deve stare al numeratore stia veramente al numeratore, e idem per il denominatore!

  4. Ovviamente, il campo di una singola carica deve andare come 1/r^2! Eppure un bel po’ di studenti consegnano codice che non segue neppure questa semplice proprietà…

  5. Quando calcolate la distanza d tra due posizioni, assicuratevi di restituire d e non d^2 (errore molto comune!).

• Stranamente, ogni anno più di uno studente sbaglia a implementare operator+ per i vettori, e invece di calcolare z = v + w calcola in realtà z = v + v = 2v, oppure z = w + w = 2w.

• Nel leggere la posizione x y z a cui calcolare il campo del dipolo da linea di comando, assicuratevi di usare la funzione std::stod oppure std::atof, anziché std::stoi o std::atoi, perché queste ultime due restituiscono valori interi.